 |
|
Задания для самостоятельной работы по теме 4.
Задание 1. Используя таблицы истинности, проверить эквивалентность булевых формул. Определить существенные и фиктивные переменные.
-
 .
. -

-
 .
. -
 .
. -
 .
. -
 .
. -
 .
. -
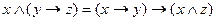 .
. -
 .
. -
 .
.
Задание 2. Для данной формулы булевой функции
а) найти СДНФ, СКНФ методом равносильных преобразований;
б) найти СДНФ, СКНФ табличным способом (сравнить с п. “а”);
в) составить полином Жегалкина;
г) составить переключательную схему.
1. ((x Ú y)→  ) Ú xÙyÙz
2. ( ) Ú xÙyÙz
2. (  )
3. (x →(zÙ(y « x)))
4. ( )
3. (x →(zÙ(y « x)))
4. (  ) → (xÚz)
5. ( ) → (xÚz)
5. ( 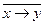 ) Ú (y→ z)
6. (xÙy) → (( ) Ú (y→ z)
6. (xÙy) → ((  ) « x)
7. (y →x) « (x → z)
8. (xÙ ) « x)
7. (y →x) « (x → z)
8. (xÙ  ) → (( ) → ((  Úz) Ù y)
9. ( Úz) Ù y)
9. (  ) → (xÚz)
10. ( ) → (xÚz)
10. (  ) → ((xÚz) → y)
11.x →(y → (z → yÙz))
12. ((yÙ ) → ((xÚz) → y)
11.x →(y → (z → yÙz))
12. ((yÙ  ) → (xÚ ) → (xÚ  )) → y
13. ( )) → y
13. ( 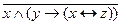 )
14. (x →(xÙ(yÚ )
14. (x →(xÙ(yÚ  Úx)))
15. ( Úx)))
15. (  ) Ú ( ) Ú (  ) )
| 16. (  ) → (xÚz)
17. xÙy → ( ) → (xÚz)
17. xÙy → (  Ùz → (xÚy))
18. (y →x) « ( Ùz → (xÚy))
18. (y →x) « (  → z)
19. (xÙ → z)
19. (xÙ  → z) → (x « z)
20. ( → z) → (x « z)
20. ( 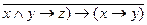 21. 21.  →(y → (z «x))
22. yÙ →(y → (z «x))
22. yÙ  → (xÚ → (xÚ  Ùy)
23. ( Ùy)
23. (  ))
24. x →(xÙ(yÚ ( ))
24. x →(xÙ(yÚ (  )))
25. ( )))
25. ( 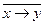 ) Ú ( ) Ú (  )
26. ( )
26. (  ) → ( ) → (  )
27. ( )
27. ( 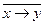 ) → (xÙz)
28. x →(z →(x Ú yÙz))
29. xÙ(y →(z « y))
30. ( ) → (xÙz)
28. x →(z →(x Ú yÙz))
29. xÙ(y →(z « y))
30. (  ) Ú (y « z) ) Ú (y « z)
|
Задание 3. Для булевой функции, заданной вектором значений, определить: 1) СДНФ, 2) СКНФ, 3) полином Жегалкина.
| 1. (10110011). | 4. (00110011). | 7. (10100011). |
| 2. (00100111). | 5. (00110001). | 8. (11100001). |
| 3. (10101011). | 6. (01100011). | 9. (11100011). |
10. (11101011).
Задание 4.Определить, является ли заданная булева функция самодвойственной, монотонной, линейной.
1) 
| 2) 
|
3) 
| 4) 
|
5) 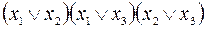
| 6) 
|
7) . 
| 8) 
|
9) 
| 10) 
|
11) 
| 12) 
|
Задание 4. Выяснить, является ли система функций A функционально полной.
1)  . .
| 2)  . .
|
3)  . .
| 4) 
|
5) 
| 6) 
|
7) 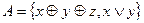 . .
| 8) 
|
9) 
| 10) 
|
11) 
| 12) 
|
13) 
| 14) 
|
15) 
| 16) 
|
17) 
| 18) 
|
Контрольные вопросы по теме 4.
1. Выберите правильный вариант ответа 1 – 4 для следующих вопросов:
а) Сколько существует различных булевых функций n переменных? б) Сколько существует различных наборов переменных для булевой функции n переменных?
Варианты ответа: 1) 2n; 2) 2*2  ; 3) n2; 4) n!.
; 3) n2; 4) n!.
2. Какое из следующих утверждений верно:
а) Переменные булевой функции и сама булева функция принимают значения 0 или 1;
б) Переменные булевой функции принимают значения 0 или 1, а значения самой булевой функции совпадают с множеством действительных чисел;
в) Значения переменных булевой функции совпадают с множеством действительных чисел, а сама булева функция принимает значения 0 или 1;
г) Значения переменных булевой функции и значения самой функции совпадают с множеством действительных чисел;
3. Выберите правильный вариант ответа 1 – 4 для следующих вопросов:
а) Сколько может быть различных ДНФ у булевой функции?
б) Сколько может быть различных СДНФ у булевой функции?
в) Сколько может быть различных КНФ у булевой функции?
г) Сколько может быть различных СКНФ у булевой функции?
Варианты ответа:
1 – ноль или одна; 2 – ноль или бесконечно много; 3 – ноль или одна; 4 – одна; 5 – одна или бесконечно много.
4. В какой из нормальных форм (ДНФ, СДНФ, КНФ, СКНФ) находится данная формула булевой функции трех переменных f(x, y, z):
а) xÚy  z; б) x
z; б) x  y
y  z; в) (xÚy)
z; в) (xÚy)  (xÚ
(xÚ  ); г) xÚyÚz; д)
); г) xÚyÚz; д) 
 y
y  z Ú y
z Ú y 
 ; е) xÚ
; е) xÚ  ; ж) x
; ж) x  z.
z.
Тема 5. Основные понятия теории графов.
Основные понятия теории графов.
Язык графов используется в ряде математических разделов, таких, например, как теория управляющих автоматов, теория алгоритмов, теория цепей Маркова. Широко применяется язык теории графов при описании моделей в экономике, биологии и других областях.
Первой работой, в которой использовалось название «граф» и давалось его точное определение, была работа Л. Эйлера, которая появилась в 1736 году в трудах Петербургской академии наук. В ней Эйлер предлагает читателю головоломку «Задача о кёнигсбергских мостах». Город Кёнигсберг (ныне Калининград) расположен на двух берегах реки Прегель и двух островах. Районы города соединены мостами (рис. 12, а). Вопрос состоит в том, можно ли, выйдя из одного района города, по одному разу пройти по каждому из мостов и вернуться в исходный район?
Л. Эйлер каждому району сопоставил вершину, каждому мосту – ребро и уже на языке графов (рис. 8, b) сформулировал задачу: существует ли циклический маршрут из последовательности ребер, выходящий из любой вершины графа и проходящий по каждому ребру в точности по одному разу?
Попытки найти такой маршрут к успеху не привели, и тогда Л. Эйлер сформулировал и доказал свою теорему: для того чтобы существовал циклический маршрут в графе G, необходимо и достаточно, чтобы граф был связным и степени всех его вершин были четными.
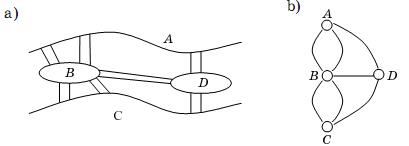
Рисунок 8. Граф переходов по мостам г. Калининграда
Приведем примеры неориентированных графов.
Таблица 4
Примеры неориентированных графов
| Граф | Вершины | Ребра |
| Семья | Люди | Родственные связи |
| Город | Перекрестки | Улицы |
| Сеть | Компьютеры | Кабели |
| Домино | Костяшки | Возможность |
| Дом | Квартиры | Соседство |
| Лабиринт | Развилки и тупики | Переходы |
| Метро | Станции | Пересадки |
| Листок в клеточку | Клеточки | Наличие общей границы |
В различных технических приложениях встречаются графы, которые существенно отличаются внешним видом, а, следовательно, и своими свойствами.
Перейдем к формальным определениям основных понятий теории графов.
Графом G = (X, А) называется упорядоченная пара множеств X = {x1, x2, …, xn} и А = {a1, a2, …, am}, где X – множество вершин, а A – множество ребер графа. Если ребра из множества A ориентированы, то они называются дугами, а граф называют ориентированным. Если ребра не имеют ориентации, то граф называют неориентированным. В противном случае граф является смешанным. На рис. 9 приведены неориентированный и ориентированный графы соответственно.
 a) a)
| X= {x1, x2, x3, x4}, A = {a1, a2, a3, a4}. |
 b) b)
| X = {x1, x2, x3, x4}, A= {a1= (x1, x2), a2= (x1, x3), a3= (x3, x4), a4= (x3, x2)}. |
Рисунок 9
Если сопоставить каждому ребру число из множества С, тогда граф называют взвешенным.
Различные ребра могут соединять одну и ту же пару вершин. Такие ребра называют кратными.Граф, содержащий кратные ребра, называется мультиграфом.
Например, кратность ребра {v1,v2} в графе, изображенном на рис. 10, равна двум, кратность ребра {v3,v4} − трем.

Рисунок 10
Неориентированное ребро графа эквивалентно двум противоположно направленным дугам, соединяющим те же самые вершины.
Ребро может соединять вершину саму с собой. Такое ребро называется петлей. Граф с кратными ребрами и петлями называетсяпсевдографом.
Множество ребер графа может быть пустым. Множество вершин графа не может быть пустым.
Пример 1.
На рис. 11 изображен ориентированный граф G = (X, A). X = {x1, x2,x3, x4},A=  .
.

Рисунок 11
Как в случае ориентированного, так и в случае неориентированного ребра говорят, что вершины xи yинцидентныребру a, если эти вершины соединены a.
Две вершины называются смежными, если они инцидентны одному и тому же ребру. Два ребра называются смежными, если они имеют общую вершину.
Степеньюr вершины графа называется число ребер, инцидентных этой вершине. На рис. 13 r(v3)=5, r(v2)=4. Вершина, имеющая степень 0, называется изолированной, а степень 1 – висячей.
Для ориентированного графа множество вершин, в которые ведут дуги, исходящие из вершины х, обозначают G(х), то есть G(х) = { y: ( x y )  G}. Множество G(x) называют образомвершины x. Соответственно G-1(у)– множество вершин, из которых исходят дуги, ведущие в вершину у, G-1(y)= {x: ( x , y )
G}. Множество G(x) называют образомвершины x. Соответственно G-1(у)– множество вершин, из которых исходят дуги, ведущие в вершину у, G-1(y)= {x: ( x , y )  G}. Множество G-1(у)называют прообразом вершины y.
G}. Множество G-1(у)называют прообразом вершины y.
Полустепенью исхода (захода) вершины x ориентированного графа G называется число d+(x) (d-(x)) дуг ориентированного графа G, исходящих из x (заходящих в x).
Следует заметить, что в случае ориентированного псевдографа вклад каждой петли инцидентной вершине x равен 1 как в d+(x), так и в d-(x).
Пример 2.
В графе, изображенном на рис. 13 (первый), концами ребра a1являются вершины x1, x2; вершина x2инцидентна ребрам a1, a2; степень вершины x3равна3; вершины x1и x3смежные; ребра a1и a2смежные; вершина x4висячая. В ориентированном графе, изображенном на рис.13 (второй), началом дуги a1является вершина x1, а ее концом - вершина x2; вершина x1инцидентна дугам a1и a2; G(x1) = {x2, x3}, G(x2) =Æ, G-1(x3) = {x1}, G-1(x1) = Æ.
Подграфомнеориентированного графа G называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G. Аналогично определяется подграф ориентированного графа. Подграф называется собственным, если он отличен от самого графа,
Граф G = (X, A)- полный, если для любой пары вершин xi и xj существует ребро (xi, xj).
Граф G = (X, A)- симметрический, если для любой дуги (xi, xj) существует противоположно ориентированная дуга(xj, xi).
Граф G = (X, A) -планарный, если он может быть изображен на плоскости так, что не будет пересекающихся дуг.
Неориентированный граф G = (X, A)– двудольный, если множество его вершин X можно разбить на два такие подмножества X1и X2, что каждое ребро имеет один конец в X1, а другой в X2.
Основные виды графов показаны на рис. 12.

Рисунок 12. Основные виды графов:
а – обычный граф;
b – граф с кратными ребрами;
c – граф с петлями и вложенными петлями;
d – «нуль-граф» – граф, не имеющий ребер, но имеющий вершины);
e – «полный граф» – граф, у которого все вершины связаны со всеми остальными;
f – граф типа «дерево», т. е. граф, у которого нет внутренних циклов;
g – направленный граф, у которого переходы из вершины в вершину имеют направления
Встречаются и различные комбинации приведенных графов, например графы с кратными ребрами и петлями, графы с направленными и ненаправленными переходами (ребрами) и т. п.