Главная | Обратная связь

Основные свойства матриц смежности и инцидентности

1. Матрица смежности неориентированного графа является симметричной. Для ориентированного графа это, вообще говоря, неверно.

2. Сумма элементов i - ой строки или i -го столбца матрицы смежности неориентированного графа равна степени вершины x_i.

3. Сумма элементов i - ой строки матрицы смежности ориентированного графа равна числу дуг, исходящих из x_i.

4. Сумма элементов i - го столбца матрицы смежности ориентированного графа равна числу дуг, входящих в вершину x_i.

5. Сумма строк матрицы инцидентности ориентированного графа является нулевой строкой.

3. Списки смежности.

Обозначим Г(x)={i / (x,i) A} – множество концов ребер, начинающихся в x (для орграфа). Для графа это множество вершин, смежных с вершиной x.

Пронумеруем все вершины графа к=1, 2, …, n. Будем рассматривать все вершины по порядку и для каждой вершины k составлять список Г(x). Все такие списки подряд без пропусков разместим в некотором массиве А. в другом массиве В, состоящем из n элементов, будем размещать номера элементов массива А, начинающих список, соответствующий данному элементу массива В. Схематически полученная структура представлена на рис. 21.

Рисунок 21.

Указанная структура называется списком смежности.

Замечание. Некоторые списки смежности в общем случае могут быть пустыми. Если список пуст, то в массиве А он места не занимает, а соответствующий элемент в массива В заносится 0.

Пример.

1. Для графа, представленного на рис. 24, список смежности имеет следующий вид:

Вершина	B	A
А (1)			Г(А)
B (2)
C (3)			Г(В)
D (4)
E (5)			Г(С)
			Г(D)
			Г(E)

2. Рассмотрим еще один граф, представленный на рис. 22. Составим для него список смежности.

Рисунок 22.			В	А
				Г(2)
(3)				Г(3)
			Г(4)

Обычно этот способ представления оказывается наиболее экономным по памяти (количество занимаемой памяти пропорционально n+m), причем в этом представлении оказывается очень удобным держать информацию о нагрузке как на дуги (в элементах списков), так и на вершины графа (в заголовках списков). Единственным существенным недостатком этого представления является то, что отсутствует мгновенный произвольный доступ к дугам. Однако в большинстве алгоритмов вполне достаточно последовательного перебора дуг, инцидентных одной вершине, который в этом представлении осуществляется достаточно быстро.

Итак, возможны следующие различные способы задания графа:

а) посредством графического изображения;

б) указанием множества вершин и множества ребер (дуг);

в) матрицей смежности;

г) матрицей инцидентности;

д) списком смежности.

 

Связность графа

Граф называется связным, если каждая пара различных вершин может быть соединена, по крайней мере, одной цепью.

Подграфомнеориентированного графа G называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G. Подграф называется собственным, если он отличен от самого графа. Аналогично определяется подграф ориентированного графа.

Компонентой связности неориентированного графа называется его связный подграф, не являющийся собственным подграфом никакого другого связного подграфа данного графа.

Пусть A(G) – матрица смежности ориентированного псевдографа G=(X, A), где X={x₁,…, x_n}. Обозначим через A^k=[a^(k)_ij] k-ю степень матрицы смежности A(G).

Элемент a^(k)_ij матрицы A^k ориентированного псевдографа G=(X, A) равен числу всех путей (маршрутов) длины k из x_i в x_j.

Матрица достижимости ориентированного графа G − квадратная матрица T(G)=[t_ij] порядка n, элементы которой равны

Матрица сильной связности ориентированного графа D − квадратная матрица S(D)=[s_ij] порядка n, элементы которой равны

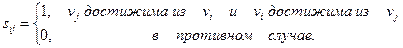
Матрица связности графа G − квадратная матрица S(G)=[s_ij] порядка n, элементы которой равны

Пример.

У неориентированного графа, изображенного на рис. 23 две компоненты связности. Первая компонента связности включает вершины x₁, x₂, x₄, x₅, а вторая состоит из одной вершины x₃.

Рисунок 23.

Матрица связности этого графа имеет вид:

S =

Мы видим, что 1-ая, 2-ая, 4-ая и 5-ая строки матрицы S одинаковы.

У ориентированного графа, изображенного на рис. 24 две компоненты сильной связности. Первая компонента связности включает вершины x₁, x₂, x₃, x₅, а вторая состоит из одной вершины x₄. Действительно, для любой пары вершин из множества {x₁, x₂, x₃, x₅} существует хотя бы один путь, соединяющий эти вершины. Например, путь (x₁, x₂, x₅, x₃, x₁) соединяет все эти вершины. Из вершины x₄ нет пути ни в одну вершину графа.

Рисунок 24.

Матрица сильной связности этого графа имеет вид:

S =

Мы видим, что 1-ая, 2-ая, 3-ая и 5-ая строки матрицы S одинаковы.