Главная | Обратная связь

Полные системы булевых функций

Система булевых функций F={f₁, f₂, … , f_n, …} называется полной, если любая булева функция может быть выражена через функции этой системы (представить в виде суперпозиции функций из функций F.

Все логические операции могут быть выражены через операции конъюнкции, дизъюнкции и отрицания, то есть класс Ф= { , , Ú} является функционально полным докажем это утверждение.

Рассмотрим два случая.

1) Пусть f тождественно не равна 0. Тогда для нее существует СДНФ, в которой для представления функции по определению используются только , , Ú. Следовательно, произвольная функция представима в заданном базисе.

2) Пусть f тождественно равна 0. Тогда для нее существует СКНФ, в которой для представления функции по определению используются только , , Ú. Следовательно, произвольная функция представима в заданном базисе.

Также полными являются следующие системы функций:

а) { , Ú}; б) { , Ù}; в) { , → }.

Полнота систем { , Ú} и { , Ù} следует из полноты системы { , , Ú}, а также законов де Моргана и двойного отрицания, следствием которых является возможность выразить конъюнкцию через дизъюнкцию и наоборот. Поэтому система { , Ù, Ú} может быть сокращена на одну функцию.

Полнота системы { , → } следует из полноты системы { , Ú} и равносильности 12, позволяющую выразить импликацию через отрицание и дизъюнкцию.

Полином Жегалкина

Всякая булева функция может быть представлена в виде полинома Жегалкина:

где , где знак + обозначает двоичное сложение (сумму по модулю 2). Таблица истинности двоичного сложения имеет вид:

 

 

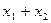
Рассмотрим два способа построения полинома.

1. Алгоритм построения полинома Жегалкина с использованием таблицы истинности.

1. Построить таблицу истинности данной булевой функции.

2. Каждому единичному значению булевой функции будет соответствовать конъюнкция , где - соответствующий набор значений переменных. Конъюнкции соединяются знаком +.

3. Заменить выражения по формуле: . Раскрыть скобки и привести подобные слагаемые по правилу: .

2. Метод неопределенных коэффициентов для построения ПЖ.

Рассмотрим этот способ на примере.

Общий вид ПЖ для функции от 2-х переменных: f(x₁, x₂)= c₁x₁x₂ + c₂x₁ + c₃x₂ + c₄.

Общий вид ПЖ для функции от 3-х переменных:

f(x₁, x₂, x₃)= c₁x₁x₂x₃+ c₂x₁x₂ + c₃ x₁x₃ + c₄x₂x₃ + c₅x₁ + c₆x₂ + c₇x₃ + c₈.

Суть метода заключается в нахождении коэффициентов c_i в приведенных формулах общего вида. Для этого по таблице истинности заданной функции определяется значение функции на заданном наборе значений переменных x₁, x₂, x_3.,Подставляя эти значения переменных и функции в разложение общего вида, определяют значение коэффициентов. После чего найденные значения коэффициентов подставляются в формулу разложения общего вида.

Пусть требуется найти полином Жегалкина для функции f(x₁, x₂)= x₁Ú x₂.

Построим таблицу истинности для заданной функции:

x1	x2	x1Ú x2

Имеем по таблице f(0,0)=0. Подставим значения переменных (0,0) в формулы разложения. Получим:

f(0, 0)= c₁00 + c₂0 + c₃0 + c₄.

Приравнивая полученные выражения (так как они представляют одну и туже функцию), получаем

f(0, 0)= c₁00 + c₂0 + c₃0 + 0=0Þ c₄=0.

Рассуждая аналогичным образом, получаем:

f(0,1)=c₁01 + c₂0 + c₃1 + 0=1Þ c₃=1;

f(1,0)=c₁10 + c₂1 + c₃0 + 0=1Þ c₂=1;

f(1,1)=c₁11 + c₂1 + c₃1 + 0=1Þ c₁=1.

Подставим найденные значения коэффициентов в разложение функции, получим:

f(x₁, x₂)= 1x₁x₂ +1x₁ + 1x₂ +0=x₁x₂ +x₁ + x₂, - полином Жегалкина для заданной функции.