Главная | Обратная связь

Двойственность. Принцип двойственности.

Функция называется двойственной к функции , если . Обозначается двойственная функция f*.

Определение 1. Функция f самодвойственна, если f= f*, т.е. двойственная функция совпадает с самой заданной функцией.

Для построения таблицы, задающей двойственную функцию из таблицы, задающей исходную функцию, необходимо выполнить следующие действия:

- столбец значений функции f инвертировать (0 заменяется на 1 и наоборот);

- затем этот столбец переписать в обратном направлении (снизу вверх).

Полученный столбец и есть значения функции f^*.

Рассмотрим некоторые функции.

1. Константы. Т.к. 1 и 0 – функции 0-арные, т.е. не имеющие аргументов, то для них построение двойственной функции сводится к построению отрицания исходной функции:

1^* = 0; 0^* = 1.

2. f(x)=x. Построим двойственную ей функцию:

f^*(x)=`f(`x) = = x = f(x), следовательно тождественная функция самодвойственна.

3. f(x)=`x. Построим двойственную ей функцию:

f^*(x)=`f(`x) = = `x = f(x), следовательно функция отрицания самодвойственна.

Символы , Ú называются двойственными.

Теорема (принцип двойственности). Если в формуле , представляющей функцию 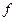, все знаки функций заменить соответственно на знаки двойственных им функций, то полученная формула 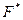будет представлять функцию , двойственную функции .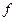

В случае, когда функция задана аналитически формулой, то для построения двойственной функции необходимо все входящие в формулу функции заменить на двойственные к ним. Если формула содержит только следующие функции {0, 1, Ù, Ú, ` }, то процесс построения двойственной функции сводиться к следующему:

· заменяется каждый 0 на 1;

· заменяется каждая 1 на 0;

· заменяется каждый знак Ù на знак Ú;

· заменяется каждый знак Ú на знак Ù;

· знаки отрицания при этом остаются без изменения.

Если функции равны, то двойственные им функции также равны, то есть если A º B, то A^* º B^*. Это позволяет с помощью принципа двойственности получать новые эквивалентные соотношения, переходя от равенства с помощью указанных замен к равенству .

Определим общее число самодвойственных функций от n переменных. Очевидно, что каждая такая функция получается определенным способом заполнения первой половины последнего столбца таблицы, задающей функцию. Всего в этом столбце 2ⁿ позиций. Произвольно заполняются половина, то есть позиций. Каждому такому заполнению соответствует одна самодвойственная функция. Следовательно всего самодвойственных функций от n переменных существует штук.

 

Нормальные формы.

Элементарной конъюнкцией называется конъюнкция (возможно одночленная), составленная из переменных или отрицаний переменных.

Пример 6.

x, y, x y, ₁ x_{2 3} – элементарные конъюнкции.

xÚy, x_{1 2} Ú ₁ x₂ – не элементарные конъюнкции.

Дизъюнктивной нормальной формой (ДНФ) называется формула, имеющая вид дизъюнкции элементарных конъюнкций (в вырожденном случае это может быть одна конъюнкция).

Пример 7.

x, x y, x Ú , ₁ x_{2 3} Ú x_{1 2} x₃ Ú x₁ x_{2 3} – ДНФ.

(xÚy) – не ДНФ.

Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, каждый конъюнктивный член которой содержит все переменные, либо их отрицания.

Пример 8.

x y, x Ú y – СДНФ функции двух переменных.

xÚ y, xÚy – не СДНФ.

Совершенная дизъюнктивная нормальная форма (СДНФ) для булевой функции , не равной тождественно нулю, имеет вид:

,

где символ 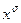определяется следующим образом:

Алгоритм построения СДНФ.

1. Построить таблицу истинности данной булевой функции.

2. Каждому единичному значению булевой функции будет соответствовать элементарная конъюнкция , где – соответствующий набор значений переменных. В конъюнкции мы записываем , если , и , если .

3. Конъюнкции соединяются знаком .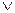

Элементарной дизъюнкцией называется дизъюнкция (возможно одночленная), составленная из переменных или отрицаний переменных.

Пример 9.

x, y, xÚy, ₁Úx₂Ú( ₃) – элементарные дизъюнкции.

x y, (x₁Ú ₂) ( ₁Úx₂) – не элементарные дизъюнкции.

Конъюнктивной нормальной формой (КНФ) называется формула, имеющая вид конъюнкции элементарных дизъюнкций (в вырожденном случае это может быть одна дизъюнкция).

Пример 10.

x, x y, x ( ), ( ₁Úx₂) ( ₃) (x₁Ú ₂Úx₃) – КНФ.

x y Ú – не КНФ.

Совершенной конъюнктивной нормальной формой (СКНФ) называется такая конъюнктивная нормальная форма, каждый дизъюнктивный член которой содержит все переменные, либо их отрицания.

Пример 11.

xÚy, (xÚ ) ( Úy) – СКНФ функции двух переменных.

x ( Úy), x y – не СКНФ.

Совершенная конъюнктивная нормальная форма (СКНФ) для функции , отличной от тождественной единицы, имеет вид:

.

Алгоритм построения СКНФ.

1. Построить таблицу истинности данной булевой функции.

2. Каждому нулевому значению булевой функции будет соответствовать элементарная дизъюнкция , где - соответствующий набор значений переменных. В дизъюнкции мы записываем , если , и , если .

3. Дизъюнкции соединяются знаком .

Теорема 2.Для каждой формулы булевой функции A имеется равносильная ей дизъюнктивная нормальная форма (ДНФ) и конъюнктивная нормальная форма (КНФ).

Доказательство теоремы состоит просто в указании алгоритмов нахождения для любой формулы A равносильных ей ДНФ и КНФ. Процесс нахождения этих форм называется приведением формулы A соответственно к ДНФ и КНФ. Для каждой формулы A имеется, вообще говоря, бесконечное множество ДНФ и КНФ, но для решения задач, в которых эти формы нужны, требуется, как правило, найти по крайней мере одну из них.

Алгоритм 1 (Алгоритм приведения формул булевых функций к ДНФ (КНФ)).

Шаг 1. Все подформулы A вида B ® C (т.е. содержащие импликацию) заменяем на ÚC или на ( ).

Шаг 2. Все подформулы A вида B « C (т.е. содержащие эквивалентность) заменяем на (A B) Ú ( ) или на (AÚ ) ( ÚB) (в соответствии с равносильностью 13).

Шаг 3. Все отрицания, стоящие над сложными подформулами, опускаем по законам де Моргана (в соответствии с равносильностями 4, 16, 17).

Шаг 4. Устраняем все двойные отрицания над формулами (в соответствии с равносильностью 8).

Шаг 5. Осуществляем раскрытие всех скобок по закону дистрибутивности конъюнкции относительно дизъюнкции для ДНФ (в соответствии с равносильностями 3а и 17) или по закону дистрибутивности дизъюнкции относительно конъюнкции для КНФ (в соответствии с равносильностью 3б).

Шаг 6. для получения более простой формулы целесообразно использовать равносильности 5, 6, 7, 9, 10, 11.

Очевидно, что в результате всех указанных операций формула имеет вид ДНФ или КНФ. Указанные операции, вообще говоря, могут осуществляться в любом порядке, однако целесообразно придерживаться изложенного выше, за исключением снятия двойных отрицаний (шаг 4), от которых следует избавляться по мере их появления.

Пример 12.

Приведем к ДНФ и КНФ рассмотренную ранее в примере 4 формулу

f(x₁, x₂, x₃) = ( ) « ( ₁Úx₂).

1. Устранив импликацию, получим:

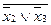( ) « ( ₁Úx₂).

2. Применив закон де Моргана к первой скобке и сняв двойные отрицания, получим:

(x₂ x₃) « ( ₁Úx₂).

3. Устранив эквивалентность, получим:

(x₂ x₃) ( ₁Úx₂) Ú ( ) ( ).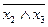

4. Применив закон де Моргана ко второму члену дизъюнкции, получим

(x₂ x₃) ( ₁Úx₂) Ú ( ₂Ú ₃) (x_{1 2}).

5. Применив закон дистрибутивности 3а, получим

(x₂ x_{3 1} Ú x₂ x₃ x₂) Ú ( ₂ x_{1 2} Ú ₃ x_{1 2}).

6. Применив законы идемпотентности 5а и 5б, и располагая переменные по возрастанию индексов, получим:

₁ x₂ x₃ Ú x₂ x₃ Ú x_{1 2} Ú x_{1 2 3}.

7. Применив 2–ой закон поглощения (6б), вместо ₁ x₂ x₃.Ú x₂ x₃ запишем x₂ x₃, а вместо x_{1 2} Ú x_{1 2 3} запишем x_{1 2} и в результате получим ДНФ нашей формулы:

f(x₁, x₂, x₃) º x₂ x₃ Ú x_{1 2}

При приведении к КНФ применим закон дистрибутивности 3б и получим:

x₂ x₃ Ú x_{1 2} º ( x₂Úx₁) (x₂Ú ₂) (x₃Úx₁) (x₃Ú ₂).

Учитывая, что. x₂Ú ₂ º 1 (равносильность 11), и применив свойство 9а, получим окончательно КНФ для f(x₁, x₂, x₃)

f(x₁, x₂, x₃) º ( x₁Úx₂) (x₁Úx₃) ( ₂Úx₃).

Приведение некоторой формулы к ДНФ и КНФ не является однозначным. Количество равносильных ДНФ и КНФ, вообще говоря, бесконечно. Однако, совершенные дизъюнктивные и конъюнктивные нормальные формы (СДНФ и СКНФ) или не существуют или единственны.

Теорема 3.Каждая формула A, не равная тождественно нулю, может быть приведена к СДНФ, которая является единственной с точностью до перестановки дизъюнктивных членов.

Теорема 4.Каждая формула A, не равная тождественно единице, может быть приведена к СКНФ, которая является единственной с точностью до перестановки конъюнктивных членов.

Доказательство этих теорем состоит в указании алгоритма приведения формулы А к СДНФ и СКНФ.