 |
|
Тема 4. Булевы функции.
Определение булевой функции
Булевой функцией f(x1, x2, ... , xn) называется произвольная функция n переменных, аргументы которой x1, x2, ... , xn и сама функция f принимают значения 0 или 1, т. е. xi 
{0, 1}, i = 1, 2, ... , n; f(x1, x2, ... , xn) {0, 1}.
Одной из важнейших интерпретаций теории булевых функций является теория переключательных функций. Первоначально математический аппарат теории булевых функций был применен для анализа и синтеза релейно-контактных схем с операциями последовательного и параллельного соединения контактов.
Любая булева функция может быть представлена таблицей, в левой части которой перечислены все возможные наборы переменных (их 2n), а в правой части – значения функции на соответствующем наборе. Пример такого задания представлен в таблице 6.
Таблица 6
| x1 x2 x3 | f(x1, x2, x3) |
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
Для формирования столбца значений переменных удобен лексико-графический порядок, в соответствии с которым каждый последующий набор значений получается из предыдущего прибавлением 1 в двоичной системе счисления, например, 100 = 011+ 1.
Всего существует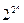 
различных булевых функций n переменных.
Функции одной переменной – f0=0 ; f1(x)=x; x)=`x; (x)=1.
Функции f0, f3 – константы, f1 – тождественная функция, f2 - функция «отрицание x» (обозначается 
). Она представлена в таблице 7.
Таблица 7
|
|
Функции двух переменных – представлены в таблице 8. Их существует всего 16 (22 
при n = 2).
Таблица 8
| x1 x2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
| 0 0 0 1 1 0 1 1 |
Рассмотрим перечисленные функции подробнее.
f0=0; f1= x1Ù x2 – конъюнкция; f2=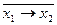 
; f3=x1; f4=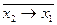 
f5=x2; f6=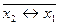 
x1+ x2 – сложение по модулю 2;
f7=x1Vx2 – дизъюнкция;
f8=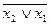 
= x1¯x2 – стрелка Пирса;
f9= x1~x2 – эквивалентность; f10= `x2; f11= x2~x1; f12= `x1; f13=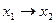 
;
f14=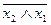 
= x1ï x2 – штрих Шеффера
f15=1