Главная | Обратная связь

Практическая работа по теме 4.

Задание 1. Определить существенные/не существенные переменные БФ. Функция задана набором значений (11110011).

Решение. Для удобства приведем таблицу истинности.

 

1	x2	x3	f(x1, x2 ,x3)

Проверим, является ли переменная ₁ существенной или фиктивной.

k=1, длина отрезка 8, половины не равны – переменная существенная.

Проверим, является ли переменная ₂ существенной или фиктивной.

k=2, длина отрезка 4, половины не равны – переменная существенная.

Проверим, является ли переменная ₃ существенной или фиктивной.

k=3, длина отрезка 2, половины равны – переменная несущественная.

 

Задание 2.Для заданной булевой функции построить двойственную функцию

Решение.

 

Задание 3.Построить СДНФ, СКНФ и полином Жегалкина для функции (11110011).

Решение. Таблица истинности данной булевой функции приведена ранее.

СДНФ имеет вид:

.

СКНФ имеет вид:

.

Построим полином Жегалкина.

Имеем функцию от 3-х переменных. Тогда общий вид ПЖ:

f(x₁, x₂, x₃)= c₁x₁x₂x₃+ c₂x₁x₂ + c₃ x₁x₃ + c₄x₂x₃ + c₅x₁ + c₆x₂ + c₇x₃ + c₈.(1)

 

1. На наборе (000):

f(000) = c₁*0*0*0+c₂*0*0+c₃*0*0+c₄*0*0+c₅*0+c₆*0+c₇*0+c₈=1 c₈=1

 

2. На наборе (001):

f(001) = c₁*0*0*0+c₂*0*0+c₃*0*0+c₄*0*0+c₅*0+c₆*0+c₇*1+c₈=1 c₇+1=1 c₇=0

 

3. На наборе (010):

f(010) = c₁*0*1*0+c₂*0*1+c₃*0*0+c₄*1*0+c₅*0+c₆*1+c₇*0+c₈=1 c₆+1=1 c₆=0

 

4. На наборе (011):

f(011) = c₁*0*1*1+c₂*0*1+c₃*0*1+c₄*1*1+c₅*0+c₆*1+c₇*1+c₈=1 c₄+ c₆+ c₇ +c₈=1

c₄+0+0+1=1 c₄=0

 

5. На наборе (100):

f(100) = c₁*1*0*0+c₂*1*0+c₃*1*0+c₄*0*0+c₅*1+c₆*0+c₇*0+c₈=0 c₅+c₈=0

c₅+1=0 c₅=1

 

6. На наборе (101):

f(101) = c₁*1*0*1+c₂*1*0+c₃*1*1+c₄*0*1+c₅*1+c₆*0+c₇*1+c₈=0 c₃+ c₅+ c₇ +c₈=0

c₃+1+0+1=0 c₃=0

 

7. На наборе (110):

f(110) = c₁*1*1*0+c₂*1*1+c₃*1*0+c₄*1*0+c₅*1+c₆*1+c₇*0+c₈=1 c₂+ c₅+ c₆ +c₈=1

c₂+1+0+1=1 c₂=1

 

8. На наборе (111):

f(111) = c₁*1*1*1+c₂*1*1+c₃*1*1+c₄*1*1+c₅*1+c₆*1+c₇*1+c₈=1

c₁+1+0+0+1+0+0+1=1

c₁+1=1 c₁=0

Подставляя найденные значения коэффициентов в уравнение (1), получим полином Жегалкина для заданной булевой функции: f(x₁,x₂,x₃)=x₁*x₂+x₁+1.

Задание 3.

1. Используя критерий полноты, определить, полна ли система F в P₂. .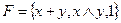

Решение. Проверим принадлежность замкнутым классам функции . Построим таблицу истинности данной функции.

, следовательно .

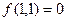, следовательно .

, следовательно, .

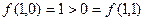, следовательно, .

Функция представляет собой полином Жегалкина первой степени, следовательно, .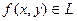

Результаты можно занести в первую строку таблицы Поста. Остальные функции исследуются аналогично.

Построим таблицу Поста для заданной системы функций:

			S	M	L
	+	-	-	-	+
	+	+	-	+	-
	-	+	-	+	+

В каждом столбце таблицы имеется минус, следовательно, система A функционально полна.

2. Выяснить, является ли заданная система булевых функций полной

Решение.

Построим таблицу истинности заданной функции:

 

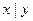
Проверим принадлежность функции основным замкнутым классам.

Очевидно (по определению), что , .

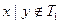Так как , то .

Найдем полином Жегалкина:

.

Следовательно, .

Так как (0,0) 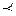(1,1), н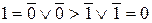о , то .

Таблица Поста для системы имеет вид.

	-	-	-	-	-

Итак, - полная система.

 

3. Выяснить, является ли заданная система булевых функций полной

	+	-	-	+	+
	-	+	-	+	+
	+	+	-	-	+
	+	+	+	+	-

Функция самодвойственна, так как

Функция немонотонная, так как (0,0,1) 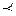(0,1,1), но 1=0+0+1>0+1+1=0.

Система - полная система.

 

4. Выяснить, является ли заданная система булевых функций полной

	-	-	+	+	-
	+	+	+	-	-

Функция самодвойственная, так как

Итак, все функции системы 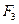целиком принадлежит классу . Следовательно, по теореме о полноте 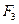не является полной.