Задания для самостоятельной работы по теме 5.

Задание 1. Решить задачу.

Задача 1. В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы было 4 телефона, каждый из которых соединен с тремя другими, 8 телефонов, каждый из которых соединен с шестью, и 3 телефона, каждый из которых соединен с пятью другими?

Задача 2. У короля 19 баронов-вассалов. Может ли оказаться так, что у каждого вассального баронства 1, 5 или 9 соседних баронств?

Задача 3. Может ли в государстве, в котором из каждого города выходит 3 дороги, быть ровно 100 дорог?

Задача 4. Джон, приехав из Диснейленда, рассказывал, что там на заколдованном озере имеются 7 островов, с каждого из которых ведет 1, 3 или 5 мостов. Верно ли, что хотя бы один из этих мостов обязательно выходит на берег озера?

Задача 5. Докажите, что число людей, когда-либо живших на Земле и сделавших нечетное число рукопожатий, четно.

Задача 6. Можно ли нарисовать на плоскости 9 отрезков так, чтобы каждый пересекался ровно с тремя другими?

Задание 2. Определите, изоморфны ли графы в парах, изображенных на рис. 35

1)	2)
3)	4)
5)

Рисунок 35.

Задание 3.Докажите, что не существует графа с пятью вершинами, степени которых равны 4, 4, 4, 4, 2.

Задание 4.Докажите, что существует граф с 2n вершинами, степени которых равны1, 1,2, 2, ..., n, n.

Задание 5.Верно ли, что два графа изоморфны, если

а) у них по 10 вершин, степень каждой из которых равна 9?

б) у них по 8 вершин, степень каждой из которых равна 3?

в) они связны, без циклов и содержат по 6 ребер?

Задание 6. В связном графе степени четырех вершин равны 3, а степени остальных вершин равны 4. Докажите, что нельзя удалить ребро так, чтобы граф распался на две изоморфные компоненты связности.

Задание 7.Задан граф списком ребер. Начертите его графическое изображение на плоскости, постройте его матрицы инциденций и смежности. Определите тремя способами число его ребер.

N ребра

Вершины

Ребра

N ребра
Вершины	A	A	B	B	C	D	D	E	E	G
Ребра	B	G	D	C	E	T	G	E	F	A

Задание 8.Построить граф заданного отношения, определить его матрицыинциденций, смежности, список смежности.

1.	r={(x, y)ÎP(A)´ P(A)/ \|x\|=\|y\|} где A={1, 2, 3};	4.	r={(x, y) Î R´R / x²+x=y²+y};
2.	r={(a, b), (c,d) )Î N²´ N²/ a+d=b+c ;	5.	r={(x, y))Î P(A)´ P(A)/ x+y конечное множество} для любого А;
3.	r={(x, y) Î R´R / x²=y²};	6.	r={(x, y)/\|x-y\|<10} на множестве N.

Задание 9. Найти минимальную линию, соединяющую города A, B, C, D, T, F. Попарные расстояния между городами заданы треугольной таблицей:

Задание 10. Постройте турнирную таблицу для 6, 8, 9 игроков.

Задание 11. Построить геометрическую реализацию графа, заданного матрицей инциденций

а)	в)
б)	г)

Задание 12. Построить коды плоских корневых деревьев, изображенных на рис. 36

Рисунок 36

Задание 13.Построить плоское корневое дерево по его коду a:

1) a=0010100111	4) a=00110101000111
2) a=0000010011011111	5) a=01001000110111
3) a=0100010110111	6) a=000101110100001011

Задание 14. По вектору a установить, является ли он кодом какого-либо плоского дерева:

1) a=001011	3) a=0110	5) a=001001
2) a=010011	4) a=00111001	6) a=0001100111

Контрольные вопросы к теме 5.

1. Какое из двух утверждений верно: а) ориентированный граф является частным случаем неориентированного графа; б) неориентированный граф является частным случаем ориентированного графа?

2. Перечислите все возможные способы задания графов.

3. Что характеризует сумма элементов столбца матрицы смежности неориентированного графа?

4. Что характеризует сумма элементов строки матрицы смежности неориентированного графа?

5. Что характеризует сумма элементов столбца матрицы смежности ориентированного графа?

6. Что характеризует сумма элементов строки матрицы смежности ориентированного графа

7. Всегда ли матрица смежности симметрична относительно главной диагонали?

8. Как по матрице смежности определить число ребер неориентированного графа?

9. Как по матрице инцидентности, не рисуя граф, определить его матрицу смежности?

10. Может ли матрица быть матрицей смежности неориентированного графа?

11. Какие из следующих утверждений являются правильными: а) если матрица смежности несимметричная, то граф ориентированный; б) если граф неориентированный, то матрица смежности симметричная; в) если диагональные элементы матрицы смежности – нули, то граф неориентированный?

12. Может ли вершина, входящая в цикл графа, иметь степень, меньшую двух?

13. Как называется путь, у которого начало первой дуги совпадает с концом последней?

14. Как называется маршрут, у которого первая вершина совпадает с последней?

15. Можно ли утверждать, что сильно связный граф всегда содержит контур?

16. Какие из следующих матриц полностью задают граф:

а) матрица инцидентности; б) матрица односторонней связности; в) матрица связности; г) матрица сильной связности; д) матрица смежности?

17. По какой матрице можно без дополнительных вычислений определить число компонент связности неориентированного графа: а) матрице смежности; б) матрице инциденций; в) матрице расстояний; г) матрице связности?

18. Может ли число компонент связности графа превосходить число его вершин?

19. Верно или неверно утверждение, что в ориентированном графе с контурами минимальный путь может содержать контуры?

20. Как называется связный граф без циклов?

21. Пусть n - число вершин, а m - число ребер в связном графе без циклов. Какие из следующих соотношений возможны:

а) n = m; б) n < m; в) n 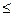m; г) n > m; д) n m?

22. Сколько ребер имеет связный граф без циклов с n вершинами?

23. Чему равно наименьшее и наибольшее число ребер в связном графе без петель и кратных ребер с n вершинами?

24. Чему равно наименьшее и наибольшее число ребер в графе без петель и кратных ребер с n вершинами?

25. Верно или неверно следующее утверждение: Минимальное остовное дерево может содержать циклы?

26. Постройте дерево наименьшей общей длины, ребра которого соединяют вершины правильного шестиугольника.

27. Сколько компонент связности может иметь дерево?

28. Можно ли построить дерево, все вершины которого имеют степень больше, чем единица?

29. Какая модель теории графов адекватна следующей задаче:

Различные организации x₁, ... , x_n обмениваются некоторой информацией (при этом связи могут быть направленными). Если между организациями x_i и x_j возможен непосредственный обмен информацией, то затраты на него составляют r_ij рублей. Возможен ли обмен информацией между двумя организациями? Если возможен, то как осуществить этот обмен с наименьшими затратами?

30. Какая модель теории графов адекватна следующей задаче:

Имеется схема городских дорог с перекрестками и, возможно, односторонним движением. Необходимо найти маршрут, соединяющий две точки на карте. Как найти такой маршрут при условии, что его длина минимальна?

31. Какая модель теории графов адекватна следующей задаче: Требуется построить схему электрической сети, в которой клеммы должны быть соединены с помощью проводов наименьшей общей длины.

32. Какая модель теории графов адекватна следующей задаче:

Имеется сеть связи, соединяющая n узлов. Если выйдут из строя некоторые каналы, то связь между узлами может быть нарушена. Какие каналы можно удалить без нарушения связи? Какие каналы нужно удалить, чтобы связь не нарушалась, а общая стоимость всех каналов была минимальной?

33. Какая модель теории графов адекватна следующей задаче:

Разрабатывается проект газопровода, соединяющего буровые скважины в Мексиканском заливе с находящейся на берегу приемной станцией. Следует выбрать проект, в котором строительство газопровода имеет минимальную стоимость.

34. Какая модель теории графов адекватна следующей задаче:

Пусть имеется n изолированных городов. Какое минимальное количество дорог между некоторыми городами надо построить, чтобы иметь возможность попасть из любого города в любой другой? Если заданы расстояния между городами, то, как выбрать сеть дорог с минимальной общей длиной?

⇐ Предыдущая 22 23 24 25 26 27 28 293031 Следующая ⇒