Главная | Обратная связь

Задания контрольной работы

Задание 1 (2 балла два примера). Построить таблицу истинности для заданной формулы. Определить для каждого высказывания, будет ли оно логически истинным, противоречивым или ни тем ни другим.

9.	Ф= (XÚY) «(ZÙY)→(XÙZ)
10.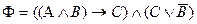
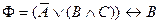
11.			Ф=
12.			Ф=(C®B)®A)®(CÚB)

 

Задание 2 (3 балла два примера). Применяя равносильные преобразования, упростить формулы.

		14.
		15.
		16.
		17.

 

Задание 3 (2 балла). На множестве натуральных чисел заданы два предиката:

1. P(x) – «число 5 делитель x»; Q(x) – «x≥17»;

2. P(x) – «x делится на 7»; Q(x) – «x≥21»;

3. P(x) – «x делится на 3»; Q(x) – «x≤9»;

4. P(x) – «число 11 делитель x»; Q(x) – «x≤121».

Найдите множества истинности следующих предикатов:

1.		3.
2.		4.

 

Задание 4 (3 балла). Составить предикат для натуральных чисел, выразив его с помощью арифметических отношений и логических связок, который принимает значение истина тогда и только тогда, когда:

6) x₁ в два раза больше x₂;

7) если x₁>0, то для всех x₃< x₂ найдутся такие x₄, что x₄+1£ x₁;

8) для всех x₁ и x₂, если x₁£x₂ и x₂<x₃, то x₁<x₃;

9) для всех x₁ и x₂, если x₁£x₂ и x₂£x₁, то x₁=x₂;

10) для всех x₁ и x₂, если неверно, что x₁<x₂ или x₃<x₂, то x₁³x₂ и x₃³x₂.

 

Задание 5 (3 балла). Решить логическую задачу.

13. У фирмы есть 100 предприятий, причем каждое предприятие выпускает хотя бы одну продукцию вида А, В или С. Продукцию всех трех видов выпускают 10 предприятий, продукцию вида А и В – 18 предприятий, продукцию вида А и С – 15 предприятий, продукцию вида В и С – 21 предприятие. Число предприятий, выпускающих продукцию вида А, равно числу предприятий, выпускающих продукцию вида В, и равно числу предприятий, выпускающих продукцию вида С. Найти число предприятий, выпускающих только продукцию вида А.

14. В студенческой группе 20 человек. Из них 10 имеют оценку «девять» по английскому языку, 8 – по математике, 7 – по физике, 4 – по английскому языку и по математике, 5 – по английскому языку и по физике, 4 – по математике и по физике, 3 – по английскому языку, по математике и по физике. Сколько студентов в группе не имеют оценок «девять»?

15. В классе 20 человек. На экзаменах по истории, математике и литературе 10 учеников не получили ни одной оценки «9», 6 учеников получили «9» по истории, 5 – по математике и 4 – по литературе, 2 – по истории и математике, 2 – по истории и литературе, 1 – по математике и литературе. Сколько учеников получили «9» по всем предметам?

16. В спортивном лагере 100 человек, занимающихся плаванием, легкой атлетикой и лыжами. Из них 10 занимаются и плаванием, и легкой атлетикой, и лыжами, 18 – плаванием и легкой атлетикой, 15 – плаванием и лыжами, 21 – легкой атлетикой и лыжами. Число спортсменов, занимающихся плаванием, равно числу спортсменов, занимающихся легкой атлетикой, и равно числу спортсменов, занимающихся лыжами. Найти это число.

 

Задание 5 (2 балла). Изобразить на координатной плоскости указанные множества:

1) ;

2) R ´{2};

3) [2;6] ´ R;

4) {4}´(3,6)/

 

Задание 6 (4 балла два примера). Установить, имеют ли место равенства:

1.		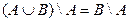5.
2.		6.
3.		7.
4.		8.

 

Задание 7 (6 баллов два примера). Задано отношение r . Найти D_r, E_r, G_r, r ^-1. Определить, какими свойствами обладает отношение.

	r={(x, y)/y=|x|} на множестве R;	5.	r={(x, y)/2x=3y} на множестве R;
	r={(x, y)/x>y2} на множестве N;	6.	r={(x, y)/x=y2} на множестве R;
	r={(x, y)/x2=y2} на множестве R;	7.	r={(x, y)/x+y<2} на множестве R;
	r={(x, y)/|x-y|<10} на множестве N;	8.	r={(x, y)/x-yÎZ} на множестве R;

 

Задание 8 (3 балла). Доказать, что заданное отношение r является отношением эквивалентности.

	r={(x, y) Î R´R / x2=y2};	13.	r={(x, y) Î R´R / x2+x=y2+y};
	r={(a, b), (c,d) )Î N2´ N2/ a+d=b+c ;	14.	r={(x, y)/|x-y|<10} на множестве N.

 

Задание 9 (4 балла 2 примера). Дана функция f(x), отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?

7.	f(x) = x3 + ex;	15.	f(x) = sinx + ;
8.	f(x) = x 2 + ;	16.	f(x) = lnx + ;
9.	f(x) = x + ;	17.	f(x) = x 2 ;
10.	f(x) = x 2 +lnx;	18.	f(x) = x 2 ;

 

Задание 10. Для данной формулы булевой функции

а) определить существенные и фиктивные переменные (2 балла);

б) найти СДНФ, СКНФ (3 балла);

в) составить полином Жегалкина (3 балла).

 

1. f(x,y,z)= 2. f(x,y,z)=x →(zÙ(y « x)) 3. f(x,y,z)= 4. f(x,y,z)=

5. 6. f(x,y,z)= 7. f(x,y,z)= 8. f(x,y,z)=

 

Задание 11 (8 баллов, таблицу заполнить всю, 2 примера). Выяснить, является ли система функций A функционально полной.

19) .	20) .
21) .	22)
23)	24)
25) .	26)

 

Задание 12. (4 балла) Граф задан матрицей инциденций. Построить геометрическую реализацию графа, список ребер и матрицу смежности.

1.	2.
3.	4.

Задание 13. (3 балла)Восстановить дерево по его коду:

1. 01001010110101

2. 00010110110010111

3. 00001011011011

4. 0101010000101111.

 

Задание 14. (4 балла) Задан граф списком ребер. Начертите его графическое изображение на плоскости, постройте его матрицы инциденции и смежности. Определите тремя способами число его ребер.

1.

2.

3.