 |
|
Геометрическая прогрессия
ГЛАВА III. РЯДЫ. РЯДЫ ФУРЬЕ
Прогрессии
Арифметическая прогрессия
Определение. Арифметической прогрессией называется числовая последовательность 
, каждый член которой, начиная со второго, равен предыдущему, сложенному с постоянным для этой последовательности числом d:
,
,
,
,
…,
,…
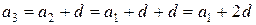Из определения следует, что любой член прогрессии может быть вычислен по формуле
для любого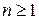 
(11.1)
Число d называется разностью или шагом прогрессии. Часто дополнительно предполагают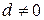 
. Если разность 
, прогрессия является возрастающей; если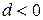 
, – убывающей.
Например: 6, 9, 12, 15,… – арифметическая прогрессия с разностью 
и первым членом 
.
Свойство арифметической прогрессии. Любой член арифметической прогрессии, начиная со второго, является средним арифметическим предыдущего и следующего члена прогрессии:
для любого 
.
Обратное также верно, т. е. это свойство является признаком арифметической прогрессии.
Сумма n первых членов арифметической прогрессии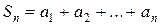 
может быть выражена формулами
(11.2)
(11.3)
Пример 11.1. Найти сумму первых ста нечётных чисел.
□Решение. Речь идет о числах 1, 3, 5, 7,… Здесь 
, 
, 
. Применим формулу (11.2):
.■
Геометрическая прогрессия
Определение. Геометрической прогрессией называется числовая последовательность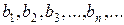 
, каждый член которой, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности число q:
,
,
,
,
…,
,…
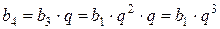Из определения следует, что любой член прогрессии может быть вычислен по формуле
для любого 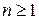(11.4)
Число q называется знаменателем прогрессии. Часто дополнительно предполагают, что 
и 
.
Например: 4, 8, 16, 32, … – геометрическая прогрессия со знаменателем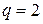 
и первым членом 
.
Свойство геометрической прогрессии. Любой член арифметической прогрессии, начиная со второго, является средним геометрическим предыдущего и следующего члена прогрессии:
для любого .
Обратное также верно, т. е. это свойство является признаком геометрической прогрессии.
Сумма n первых членов арифметической прогрессии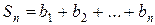 
может быть выражена формулами
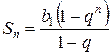(11.5)
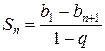(11.6)
Если разность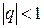 
, то прогрессия называется бесконечно убывающей геометрической прогрессией. Для неё определяется понятие суммы всех членов бесконечно убывающей геометрической прогрессии, а именно: это число, к которому неограниченно приближается сумма n первых членов рассматриваемой прогрессии при неограниченном возрастании числа n. Сумма членов бесконечно убывающей геометрической прогрессии вычисляется по формуле:
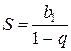. (11.7)
Пример 11.2. Найти сумму первых десяти членов последовательности 4, 8, 16, 32, …
□Решение. Здесь 
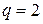, , . Применим формулу (11.5):
.■
Пример 11.3.Найти сумму членов бесконечно убывающей геометрической прогрессии 
□Решение. Здесь 
, 
. Применим формулу (11.7). Тогда
. ■
Факториал
Определение. Факториалом числа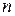 
(обозначается n!, произносится эн факториал) называется произведение всех натуральных чисел до n включительно: 
.
По определению полагают 
. Факториал определен только для целых неотрицательных чисел.
Например: 
.
Свойство факториала.Значение факториала приближенно равно
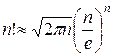(следствие асимптотической формулы Стирлинга).
Определение. Двойным факториалом числа 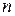(обозначается n!!, произносится эн два факториала) называется произведение всех натуральных чисел в отрезке 
, имеющих ту же четность, что и n.
Таким образом,
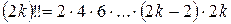и 
.
По определению полагают 
.
Например: 
, 
.
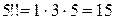Числовые ряды
Основные понятия
Определение. Числовым рядом называется выражение вида
,(12.1)
где 
– числа, называемы членами ряда, 
– общим членом ряда. Сокращённо ряд (12.1) записывают в виде
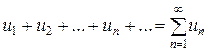. (12.2)
Ряд считается заданным, если известен общий член ряда , выраженный как функция его номера :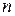 
.
Определение.Сумма 
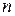первых членов ряда называется 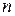-йчастичной суммой.
Определение. Суммой ряда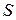 
называется предел
ой частичной суммы при 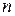стремящемся к бесконечности, т.е. 
.
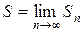Определение.Ряд называется сходящимся, если 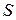– конечное число; если 
или 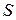не существует, то ряд называется расходящимся. Говорят, что расходящийся ряд суммы не имеет.
Нахождение суммы ряда является достаточно сложной задачей. Исключения составляют те ряды, в которых члены образуют арифметическую или геометрическую прогрессию.
Пример 12.1.Найти общий член ряда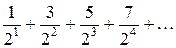 
.
□Решение.
1. Последовательность чисел в числителях 
образует арифметическую прогрессию с первым членом и разностью . Поэтому общий член для нее равен
.
2. Последовательность чисел в знаменателях 
тоже образует арифметическую прогрессию с первым членом 
и разностью 
. Поэтому общий член для нее равен
.
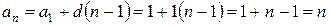Отметим, что в последовательности каждый член совпадает с его порядковым номером, поэтому общий член для нее равен .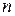
3. В итоге, общий член ряда равен 
, и ряд можно записать в сокращенном виде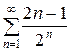 
. ■
Пример 12.2.Найти общий член ряда
.
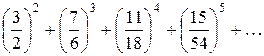□Решение.
1. Последовательность чисел в числителях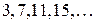 
образует арифметическую прогрессию с первым членом 
и разностью 
. Поэтому общий член для нее равен
.
2. Последовательность чисел в знаменателях 
образует геометрическую прогрессию с первым членом 
и знаменателем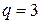 
. Поэтому общий член для нее равен
.
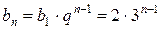3. Отметим, что в последовательности 
в степенях дробей каждый член больше своего порядкового номера на 1, поэтому общий член для нее равен 
.
4. В итоге, общий член ряда равен 
, и ряд можно записать в сокращенном виде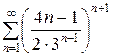 
.■
Пример 12.3.Найти общий член ряда 
.
□Решение.
1. Перепишем ряд в другом виде, заметив то, что в числителях и знаменателях находятся факториалы:
.
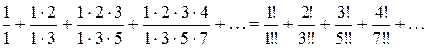2. В последовательности чисел каждый член совпадает с его порядковым номером, поэтому общий член для нее равен .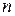
3. Последовательность чисел в знаменателях образует арифметическую прогрессию с первым членом и разностью . Поэтому общий член для нее равен
.
4. В итоге, общий член ряда равен 
, и ряд можно записать в сокращенном виде 
.■
Пример 12.4.Найти сумму ряда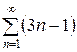
.
□Решение.
1. Выясним, образуют ли члены ряда какую-нибудь прогрессию. Для этого распишем ряд почленно: 
. Действительно, члены ряда образуют арифметическую прогрессию с первым членом 
и разностью . Поэтому сумму n первых членов ряда можно найти по формуле (11.2):
.
2. В итоге сумма ряда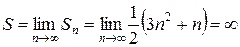 
. Следовательно, ряд расходится и суммы не имеет.■
Пример 12.5.Найти сумму ряда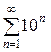
.
□Решение.
1. Выясним, образуют ли члены ряда какую-нибудь прогрессию. Для этого распишем ряд почленно: 
. Действительно, члены ряда образуют геометрическую прогрессию с первым членом 
и знаменателем 
. Поэтому сумму n первых членов ряда можно найти по формуле (11.5):
.
2. В итоге сумма ряда 
. Следовательно, ряд расходится и суммы не имеет.■
Пример 12.6.Найти сумму ряда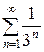
.
□Решение.
1. Выясним, образуют ли члены ряда какую-нибудь прогрессию. Для этого распишем ряд почленно: 
. Действительно, члены ряда образуют геометрическую прогрессию с первым членом 
и знаменателем 
. Поэтому сумму n первых членов ряда можно найти по формуле (11.5):
.
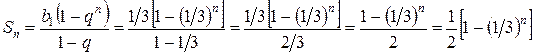2. В итоге, сумма ряда 
. Следовательно, ряд сходится и имеет сумму 
.
Замечание.Обнаружив, что для геометрической прогрессии знаменатель оказался равен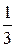 
, можно было найти сумму ряда не находя частичную сумму 
. Если знаменатель 
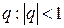, то сумма соответствующей последовательности равна 
. ■
В примерах 12.5 и 12.6 члены ряда образовывали геометрическую прогрессию. В примере 12.5 знаменатель 
равнялся 10, и ряд оказался расходящимся; в примере 12.6 знаменатель равнялся 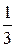, и ряд оказался сходящимся. Приведем исследование зависимости сходимости таких рядов от знаменателя с помощью нахождения их сумм.