 |
|
Знакочередующиеся ряды
Знакочередующимся рядом называется ряд вида
,
где 
для всех 
.
Теорема(достаточный признак Лейбница сходимости знакочередующегося ряда).
Знакочередующийся ряд сходится, если:
- Последовательность абсолютных величин членов ряда монотонно убывает, т.е.
- Общий член ряда стремится к нулю:
При этом сумма S ряда удовлетворяет неравенствам 
Рассмотрим сначала частичную сумму четного числа (2m) членов ряда. Имеем
Выражение в каждой скобке, согласно первому условию теоремы, положительно. Следовательно, сумма 
и возрастает с возрастанием номера 2m.
С другой стороны, 
можно переписать так:
Легко видеть, что 
. Таким образом, последовательность 
возрастает и ограничена сверху. Следовательно, она имеет предел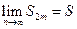 
, причем .
Рассмотрим теперь частичные суммы нечетного числа (2m+1) членов ряда. Очевидно, что 
. Отсюда следует, что 
, т.к. 
в силу второго условия теоремы. Итак, 
как при четном n, так и при нечетном n. Следовательно, ряд сходится, причем .
Общий достаточный признак сходимости знакопеременных рядов
Знакочередующийся ряд является частным случаем знакопеременного ряда. Числовой ряд 
, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным.
Для знакопеременных рядов имеет место следующий общий достаточный признак сходимости.
Теорема.
Пусть дан знакопеременный ряд
Если сходится ряд 
,
составленный из модулей членов данного ряда, то сходится и сам знакопеременный ряд .
Рассмотрим вспомогательный ряд, составленный из членов рядов и :
Очевидно, что 
для всех . Но ряд 
сходится в силу условия теоремы и свойства 1 числовых рядов. Следовательно, на основании признака сравнения сходится и ряд 
. Поскольку данный знакопеременный ряд представляет собой разность двух сходящихся рядов
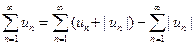
то, на основании свойства 2 числовых рядов, он сходится.
Обратное утверждение неверно.