Главная | Обратная связь

Элементы алгебры логики (8 часов)

[8], c.23 … 90

Высказывания. Основные логические операции. Булевы функции и нормальные формы. Совершенные дизъюнктивная и конъюнктивная нормальные формы. Полные системы булевых функций и базис. Нахождение сокращённой ДНФ методом Квайна. Построение минимальных ДНФ методом Петрика. Технические применения алгебры логики.

 

2.2. Тематический план дисциплины

Тематический план дисциплины

для студентов очной формы обучения

 

№ п/п	Наименование раздела, (отдельной темы)	Кол-во часов по дневной форме обучения	Виды занятий и контроля
Лекции	ПЗ(С)	Самостоятельнпя работа	Тесты	Контрольные работы	Лабораторные работы
аудит.	ДОТ	аудит.	ДОТ
ВСЕГО
	Введение
	Численные методы							№1	№1
1.1	Обработка результатов измерений и погрешности вычислений
1.2	Интерполяция и численное дифференцирование								Зад.1	Л/Р 1
1.3	Численное интегрирование								Зад.2	Л/Р 2
1.4	Приближение функций
1.5	Многомерные задачи

Тематический план дисциплины

для студентов очно-заочной формы обучения

№ п/п

Наименование раздела, (отдельной темы)

Кол-во часов по оч-заоч. форме обучения

Виды занятий и контроля

Лекции

ПЗ(С)

Самостоятельнпя работа

Тесты

Контрольные работы

Лабораторные работы

аудит.

ДОТ

аудит.

ДОТ

ВСЕГО

Введение

Численные методы

№1

№1

1.1

Обработка результатов измерений и погрешности вычислений

1.2

Интерполяция и численное дифференцирование

Зад.1

Л/Р 1

1.3

Численное интегрирование

Зад.2

Л/Р 2

1.4

Приближение функций

1.5

Многомерные задачи

1.6

Численные методы алгебры

Зад.3

Л/Р 3

1.7

Решение систем нелинейных уравнений и задач оптимизации

1.8

Численные методы решения обыкновенных дифференциальных уравнений

Л/Р 4

Теория функций комплексного переменного

№2

№2

2.1

Комплексные числа и действия над ними

0,5

Зад.4

2.2

Функции комплексного переменного. Условия Коши-Римана

0,5

Зад.5

2.3

Элементарные функции и конформные отображения

0,5

2.4

Представление регулярных функций интегралами

Зад.6

2.5

Представление регулярных функций рядами

2.6

Вычеты функций и их применения

0,5

Дискретная математика

3.1

Элементы теории графов

Зад.7

3.2

Формальные языки и дискретные автоматы

3.3

Элементы алгебры логики

Зад.8

 

Тематический план дисциплины

для студентов заочной формы обучения

 

№ п/п	Наименование раздела, (отдельной темы)	Кол-во часов по дневной форме обучения	Виды занятий и контроля
Лекции	ПЗ(С)	Самостоятельнпя работа	Тесты	Контрольные работы	Лабораторные работы
аудит.	ДОТ	аудит.	ДОТ
ВСЕГО
	Введение
	Численные методы							№1	№1
1.1	Обработка результатов измерений и погрешности вычислений
1.2	Интерполяция и численное дифференцирование								Зад.1	Л/Р 1
1.3	Численное интегрирование								Зад.2	Л/Р 2
1.4	Приближение функций
1.5	Многомерные задачи
1.6	Численные методы алгебры								Зад.3	Л/Р 3
1.7	Решение систем нелинейных уравнений и задач оптимизации
1.8	Численные методы решения обыкновенных дифференциальных уравнений									Л/Р 4
	Теория функций комплексного переменного							№2	№2
2.1	Комплексные числа и действия над ними		0,5						Зад.4
2.2	Функции комплексного переменного. Условия Коши-Римана		0,5						Зад.5
2.3	Элементарные функции и конформные отображения

 

 

 

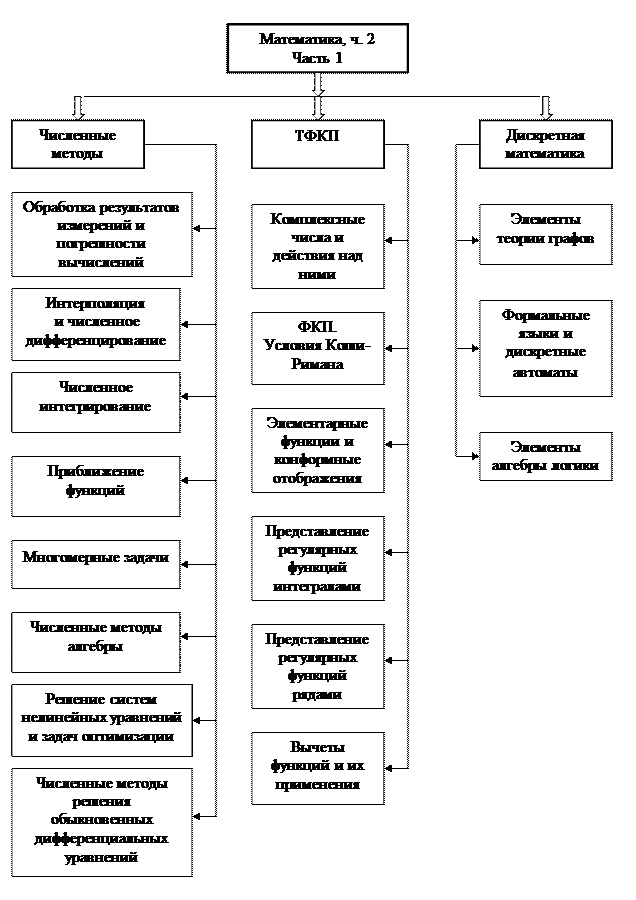
2.3. Структурно-логическая схема дисциплины

2.4. Временной график изучения дисциплины при использовании информационно-коммуникационных технологий

 

№	Название раздела (темы)	Продолжительность изучения раздела (темы) в днях (из расчета – 4 часа в день)
1.	Численные методы
2.	ТФКП	17,5
3 .	Дискретная математика
Итого:		37,5

 

2.5. Практический блок

Практические занятия

Номер и название раздела (темы)	Наименование практических занятий	Кол-во часов
Ауд.	ДОТ
1. Численные методы	Численные методы в инженерных расчётах
2. ТФКП	Задачи по теории функций компл. переменного
3. Дискретная математика	Теория графов, дискр. автоматы, алгебра логики