Главная | Обратная связь

Обработка результатов измерений и погрешности вычислений

Изучаемые вопросы: Источники и классификация погрешности. Запись чисел в ЭВМ. Абсолютная и относительная погрешности. Формы записи данных. О вычислительной погрешности. Погрешности функций.

 

После изучения этой темы Вам следует ответить на вопросы для самопроверки.

 

Следует различать погрешности измерений и погрешности решения задач. Первые изучаются в физике, а вторые обуславливаются несколькими причинами: неточностью модели, описывающей то или иное явление, неточностью метода решения и неточностью данных на этапе ввода их для решения, или вывода результатов округления. Поэтому говорят о неустранимых погрешностях, погрешностях метода и вычислительных погрешностях.

Если – точное значение некоторой величины, а 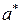– приближённое, то абсолютной погрешностью приближённого значения 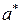называют величину 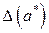, про которую известно, что

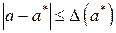. (1)

Относительной погрешностью приближённого значения 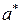называют величину 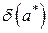, про которую известно, что

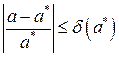. (2)

Часто её выражают в процентах.

Абсолютную и относительную погрешности принято записывать в виде числа, содержащего одну или две значащие цифры в форме

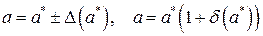. (3)

Например,

 

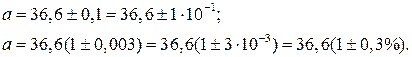
Пример 1. ○Абсолютная и относительная погрешности числа .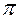

Число 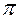– трансцендентное число, равное 3,1415926… . Приближённое значение 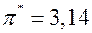. Граница абсолютной погрешности 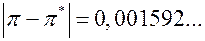, или, с учётом (3), 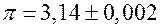. Граница относительной погрешности .●

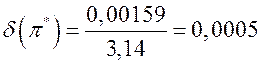Значащими цифрами числа 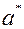называют все цифры в его записи, начиная с первой ненулевой слева.

Пример 2. ○Подчёркнуты значащие цифры в следующих числах:

0,573; 24,0350; 0,0025400.●

Значащая цифра числа 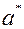называется верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.

Пример 3. ○Верные цифры числа 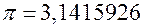подчёркнуты:

Если 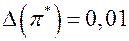, то верных цифр в числе три: 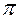= 3,1415926,

если 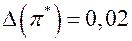, то верных цифр в числе две: 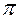= 3,1415926,

если 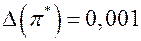, то верных цифр в числе четыре: 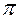= 3,14115926. ●

Для оценки погрешности арифметических действий используют следующие правила.

Абсолютные погрешности суммы или разности не превосходят абсолютной погрешности их членов:

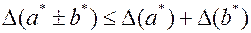(4)

Относительные погрешности в этом случае

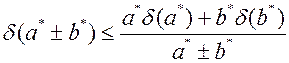(5)

Абсолютные погрешности произведения и частного рассчитывают по формулам

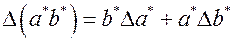и (6)

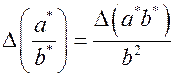(7)

соответственно. Их относительные погрешности равны:

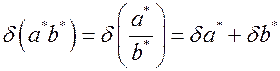. (8)

В частности,

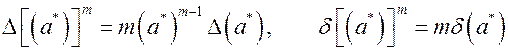. (9)

 

Пример 4. Вычислить и определить погрешности результата.

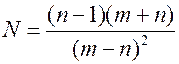, где .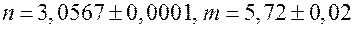

○Имеем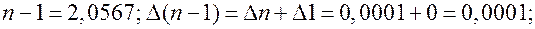

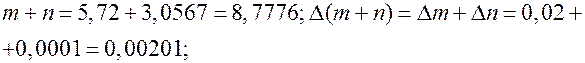
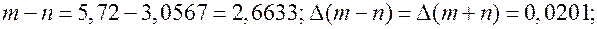
Тогда

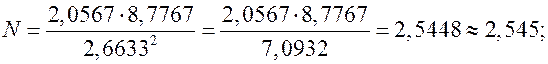
Относительная погрешность

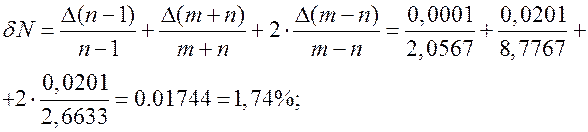
Тогда абсолютная погрешность равна .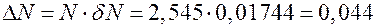

Итак, . ●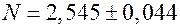

 

Существенную часть теории численных методов составляет построение устойчивых алгоритмов, использование которых ведёт к искажению результатов вычислений с погрешностью, находящейся в заданных пределах. В этом случае говорят о вычислительной погрешности. Например, потеря значащих цифр происходит при вычитании близких больших чисел. Если такие числа округлить с большой абсолютной погрешностью, то результат вычитания их также даст большую абсолютную погрешность. Во избежание этого такие расчёты следует проводить с двойной точностью.

Следует помнить, что предельная абсолютная погрешность суммы или разности равна сумме предельных погрешностей, а предельная относительная погрешность произведения или частного равна сумме предельных относительных погрешностей.

 

Подробнее об этой теме можно узнать из [7], c.17-34.

Вопросы для самопроверки по теме 1.1

 

1. Что такое абсолютная и относительная погрешности?

2. Можно ли выражать погрешность в процентах? Какую погрешность?

3. В какой форме записывают абсолютную и относительную погрешности?

4. Чему равны погрешности суммы и разности, а также произведения и частного? О каких погрешностях в данных случаях идёт речь?