Главная | Обратная связь

Метод касательных (Ньютона)

Уточнение корней – это доведение их до заданной степени точности. Существует несколько методов уточнения корней: метод половинного деления, метод хорд, метод касательных, комбинированный метод хорд и касательных, метод итераций. Рассмотрим уточнение корней методом касательных.

В дальнейшем будем считать, что функция f(x) непрерывна на промежутке [a, b], искомый корень х* отделен на этом промежутке и является единственным.

Суть метода касательных заключается в том, что на промежутке [a, b] дуга кривой y = f(x) заменяется касательной к этой кривой. За приближенное значение корня принимается точка пересечения касательной с осью х(рис. 6, 7). Возможны следующие варианты:

Вариант 1. f(a) < 0, f(b) > 0, f'(x) > 0, f''(x) > 0, т.е. функция монотонно-возрастающая, график функции – выпуклый вниз (рис. 6). Касательная к кривой в точке b пересекает ось х в точке с₁, которая и принимается за первое приближение корня х₁. Уравнение касательной к кривой в точке b есть

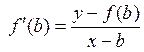(1)

 

Найдем значение x = x₁, для которого y = 0.

 

Эта формула носит название формулы метода касательных.

 

		f(a) > 0, f(b) < 0,   f'(x) < 0, f''(x)< 0
	f(a) < 0, f(b) > 0,   f'(x) > 0, f''(x) > 0

 

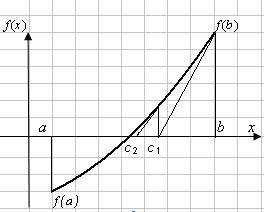
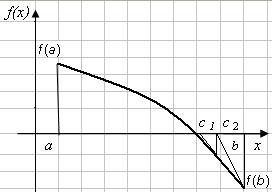
Рис. 6 Рис. 7

 

Теперь корень (первое приближение) находится внутри отрезка [a, c₁]. Если значение корня не устраивает, его можно уточнить, применяя метод касательных к отрезку [a, c₁]: построим касательную к кривой в точке с₁. Она пересекает ось х в точке с₂. Точка пересечения касательной с осью х, принимается за второе приближение корня − х₂.

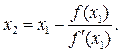
Продолжая этот процесс, находим

(2)

 

Процесс уточнения продолжается до тех пор, пока не будет получен приближенный корень с заданной точностью ε, т.е. до тех пор, пока корень не будет отделен на отрезке [x_n-1 - x_n], для которого выполняется условие

|x_n-1 - x_n | < ε.

 

По формуле (2) корни вычисляются и для случая, когда f(a) > 0, f(b) < 0, f'(x) < 0, f''(x) < 0, т.е. функция монотонно-убывающая, а график функции – выпуклый вверх (рис. 7).

 

Вариант 2. f(a) > 0, f(b) < 0, f'(x) < 0, f''(x) > 0, т.е. функция монотонно-убывающая, а график функции – выпуклый вниз (рис. 8).

Касательная к кривой в точке f(а) пересекает ось х в точке с₁, которая принимается за первое приближение корня х₁. Уравнение хорды есть

 

(3)

	f(a) > 0, f(b) < 0,   f'(x) < 0, f''(x) > 0
		f(a) < 0, f(b) > 0,   f'(x) > 0, f''(x) < 0

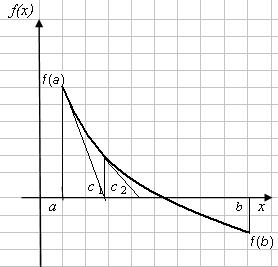
Рис. 8 Рис. 9

 

Найдем значение x = x₁, для которого y = 0.

 

 

или в общем виде

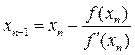. (4)

 

Процесс уточнения продолжается до тех пор, пока не будет получено приближенное значение корня с заданной точностью ε.

По формуле (4) корни вычисляются и для случая, когда f(a) < 0, f(b) > 0, f'(x) > 0, f''(x) < 0, т.е. функция монотонно-возрастающая, график функции – выпуклый вверх (рис. 9).

 

На основании полученных выражений можно сформулировать правило: за исходную точку следует выбирать тот конец отрезка, для которого знак функции совпадает со знаком второй производной. В первом случае f(b)· f''(x) > 0, в качестве начального приближения берем точку b = x₀ и используем формулу (2); во втором случае – f(a)· f''(x) > 0, в качестве начального приближения берем точку a = x₀ и используем формулу (4).

Пример (продолжение). □Уточнить корни уравнения f(x) = x³ -8x + 2, отделенные на отрезках [-3, -2], [0, 1], [2, 3] методом касательных с точностью ε = 0,005.

Решение.

1) Уточним корень уравнения f(x) = x³ -8x + 2, отделенный на отрезке [-3, -2].

f(a) = f(-3) = -1, f(b) = f(-2) = 10, f'(x) > 0, f''(x) < 0 (см. табл. 3 и рис. 9), поэтому в качестве начального приближения возьмем точку a = -3 и используем для вычислений формулы (3) и (4), вспомогательные вычисления выполним в таблице (табл. 4) или реализуем в таблице Excel (рис. 11, 11-а).

Таблица 4

Рис.10(режим решения)

 

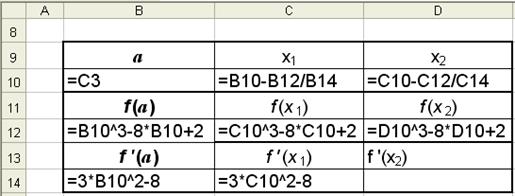
Рис. 10-а (режим формул)

 

.

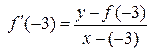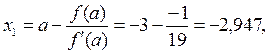|-2,947 – (-3)| = 0,053;

0,053 > 0,005.

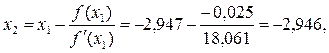|-2,946 – (-2,947)| = 0,001;

0,001 < 0,005,

следовательно, x = -2,946 − первый искомый корень уравнения f(x) = x³ -8x + 2, вычисленный методом касательных с точностью ε = 0,005.●