Главная | Обратная связь

Понятие о решётчатых функциях и разностных уравнениях.

Дискретная САУ получает входную информацию и выдаёт выходную информацию в дискретные моменты времени. Поэтому при исследовании дискретных систем рассматривается их поведение только в дискретные моменты времени nT₀, где Т₀ такт счёта, n=0,1,2,… — номер такта счёта. Для этого вводится понятие решётчатых функций.

Решётчатой называют функцию, которая существует лишь в дискретные равноотстоящие друг от друга значения времени и в промежутках между этими значениями равна нулю. На рис. 2.3.1 сплошными вертикальными линиями показана решетчатая функция f[nT₀].

 

 

 

Рисунок 2.3.1.

 

Непрерывной функции (пунктирная кривая) соответствует одна и только одна решётчатая функция, а одной решётчатой функции соответствует бесконечное количество непрерывных функций.

Часто в цифровых САУ используется безразмерное время. Пусть безразмерное непрерывное время определено выражением

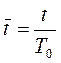, (2.3.1)

тогда безразмерное дискретное время будет

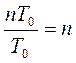, n=0,1,2,… (2.3.2)

Непрерывные системы обычно описываются дифференциальными уравнениями. Дискретные системы описываются разностными уравнениями. Рассмотрим разностные уравнения и их соотношения с дифференциальными уравнениями. Для операции дифференцирования можно записать

,

т.е. операции дифференцирования с точностью до коэффициента 1/Т₀ соответствует операция вычитания (разность).

В безразмерном времени разности обозначают так:

– первая прямая разность,

– первая обратная разность, (2.3.3)

где 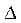- оператор «дельта», 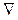- оператор «набла».

Аналогом второй производной по времени являются вторая прямая и обратная разности.

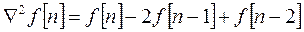. (2.3.4)

Аналогично можно получить разности более высоких порядков.

Дискретным аналогом интеграла является полная сумма

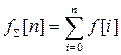. (2.3.5)

Выше была установлена связь между производной и конечными разностями и интегралом и суммой. Дифференциалы и интегралы используются для описания систем в непрерывном времени в виде дифференциальных и интегральных уравнений. Поведение дискретной системы в дискретные моменты времени описывается разностными уравнениями. Разностными уравнениями можно описать и непрерывную систему, но её поведение будет характеризоваться только в дискретные моменты времени. Рассмотрим связь между дифференциальными и разностными уравнениями на примере

.

С помощью полученных выше соотношений составляем разностное уравнение, используя обратные разности

или

,

или

,

где

, .

Если f[n]=0, то разностное уравнение называется однородным, если f[n]¹0, то разностное уравнение называется неоднородным.

В общем случае разностное уравнение можно представить в виде

(2.3.6)

(6) — разностное уравнение к-го порядка. Для решения необходимо знать начальные условия, т.е. значения y(n) в предыдущие моменты времени y(0), y(1), y(k-1).

В дифференциальных уравнениях для сведения к алгебраическому уравнению используют оператор дифференцирования . Для решения разностного уравнения путём сведения его к алгебраическому уравнению используют оператор сдвига z, так что

и т.д… (2.3.7)

С помощью оператора сдвига уравнение (6) перепишется в виде

, (2.3.8)

откуда формально можно записать

, (2.3.9)

где ─ передаточная функция дискретной системы. Если в W(z) знаменатель приравнять к нулю, то получится характеристическое уравнение, соответствующее разностному уравнению (6).

(2.3.10)