Главная | Обратная связь

Частотные характеристики дискретных систем

С частотными характеристиками дискретных систем сталкиваются при рассмотрении установившейся реакции дискретной цепи на входной сигнал в виде гармонической решётчатой функции, а также при исследовании устойчивости дискретных систем. Гармоническая решётчатая функция имеет вид

(2.11.1)

На рис. 1 представлен график функции (1)

Рисунок 2.11.1. Гармоническая решеточная функция

На рис. 1 приняты следующие обозначения: Т – период гармонической функции; Т₀ – такт счёта. Соответствующие частоты квантования и гармонической функции определяются выражениями

. (2.11.2)

В непрерывных системах для исследования их частотных свойств теоретически рассматривают диапазон частот от нуля до бесконечности, а на практике в рабочей полосе частот, которая всё равно является широкой. Определим, в каком диапазоне частот надо исследовать частотные характеристики дискретных систем. Для этого в функции (1) дадим приращение частоты величиной kw₀ , где k – целое число.

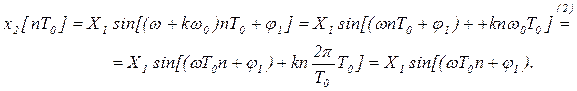(2.11.3)

Сравнивая выражения (1) и (3), приходим к выводу, что при k=1,2,… функции х₁, и х₂ совпадают. Отсюда можно заключить, что для исследования частотных свойств дискретных систем достаточно рассмотреть диапазон частот от нуля до w₀.

В непрерывных системах для получения частотных характеристик надо в передаточную функцию сделать подстановку p=jw. В дискретных системах для получения частотных характеристик надо в передаточную функцию сделать подстановку

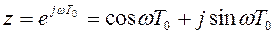. (2.11.4)

В результате получим

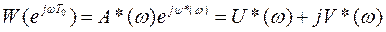, (2.11.5)

где A*(w); y*(w) – АЧХ и ФЧХ дискретной системы;

U*(w); V*(w) – действительная и мнимая части АФЧХ.

На основании (3), (5) можно заключить, что все частотные характеристики достаточно рассмотреть в диапазоне частот от нуля до w₀. Построение АФЧХ, АЧХ, и ФЧХ производится, в функции частоты . Построение ЛАЧХ и ЛФЧХ производится, как правило, в функции псевдочастот 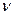и l, т.к. при этом сохраняются асимптотические свойства ЛАЧХ. Для перехода к псевдочастотам применяется 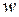-преобразование по зависимостям

. (2.11.6)

(См. аппроксимацию Тастина (2.10.9)). Переходя к частотной функции заменой (4), получим

, (2.11.7)

где 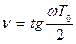- относительная псевдочастота.

Для получения абсолютной псевдочастоты используют зависимость

.

При достаточно малом 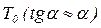можно записать

,

т.е. при достаточно малом Т₀ абсолютная псевдочастота совпадает с несущей частотой w (с частотой гармонического сигнала), т.е. при достаточно матом Т₀ частотные характеристики дискретных и непрерывных систем близки.