Главная | Обратная связь

Z-преобразование (дискретное преобразование Лапласа).

Выше разностные уравнения были получены из дифференциальных уравнений приближённым методом с помощью конечных разностей. Для получения точных разностных уравнений используется z-преобразование или дискретное преобразование Лапласа. Если для непрерывных систем используется обычное преобразование Лапласа

, (2.4.1)

то дискретное преобразование Лапласа в безразмерном времени имеет вид

(2.4.2)

В размерном времени

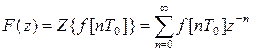(2.4.3)

Функция f[nT₀] называется оригиналом, а F[z] её z–отображением, Z – символ преобразования.

С помощью z-преобразования разностные уравнения приводятся к алгебраическим уравнениям, которые решаются гораздо легче, чем разностные, а затем к полученным решениям применяют обратное z-преобразование, которое обозначается так:

, (2.4.4)

в результате чего получаем разностные уравнения.

Найдём преобразования простейших функций времени.

1) единичная ступенчатая функция

.

Последнее выражение представляет собой геометрическую прогрессию.

2) линейная функция времени

.

Аналогичным образом можно найти z-отображения и других функций времени.

Для решения разностных уравнений надо находить z-отображения не только для функций времени, состоящих в правой части уравнения, а и для искомых функций, которые обычно записываются в левых частях разностных уравнений.

Для их преобразования используют ряд свойств. Рассмотрим некоторые из них.

Некоторые основные свойства z–преобразования.

1) свойство линейности:

(2.4.5)

2) теорема сдвига.

Если временное запоздание t равно целому числу m тактов счёта Т₀,

(2.4.6)

— формула сдвига вправо.

(2.4.7)

— формула сдвига влево.

 

Изображение прямых и обратных разностей.

(2.4.8), (2.4.9)

Теорема о начальном и конечном значении оригинала.

(2.4.10), (2.4.11)

Теорема свёртки.

, (2.4.12)

где (2.4.13)