|
|
Второе начало термодинамики и «тепловая смерть Вселенной»
Вселенная, весь мир, безграничный во времени и пространстве и бесконечно разнообразный по тем формам, которые принимает материя в процессе своего развития (рис. 133).

Рис. 133.
На современном этапе существования (13,72 млрд лет) Вселенная излучает как абсолютно чёрное тело с температурой 2,725 К. Максимум спектра излучения приходится на частоту 160,4 ГГц (микроволновое излучение), что соответствует длине волны 1,9 мм. Оно изотропно с точностью до 0,001 %.
Тепловая смерть — термин, описывающий конечное состояние любой замкнутой термодинамической системы, и Вселенной в частности. При этом никакого направленного обмена энергией наблюдаться не будет, так как все виды энергии перейдут в тепловую. Термодинамика рассматривает систему, находящуюся в состоянии тепловой смерти, как систему, в которой термодинамическая энтропия максимальна.
Вывод о «тепловой смерти» Вселенной был сформулирован Р. Клаузиусом в 1865 г. на основе второго начала термодинамики. Согласно второму началу термодинамики, любая физическая система, не обменивающаяся энергией с другими системами (для Вселенной в целом такой обмен, возможно, исключен), стремится к наиболее вероятному равновесному состоянию с максимумом энтропии. Такое состояние соответствовало бы «тепловой смерти» Вселенной.
Второе начало термодинамики иногда используется критиками эволюции с целью показать, что развитие природы в сторону усложнения невозможно. Подобная интерпретация физического закона неверна: ведь энтропия не убывает только в замкнутых системах.
Ещё до создания современной космологии были сделаны многочисленные попытки опровергнуть вывод о тепловой смерти Вселенной. Наиболее известна из них флуктуационная гипотеза Л. Больцмана (1872 г.), согласно которой Вселенная извечно пребывает в равновесном изотермическом состоянии, но по закону случая то в одном, то в другом её месте иногда происходят отклонения от этого состояния; они происходят тем реже, чем большую область захватывают и чем значительнее степень отклонения.
Современная физика находит выход из этой ситуации: по мнению Л.Ландау[47] общая теория относительности рассматривает Вселенную как систему, находящуюся в переменном гравитационном поле, и в таких условиях закон возрастания энтропии неприменим. А. Фридман[48] доказал, что Вселенная, заполненная тяготеющим веществом, не может быть стационарной, а должна расширяться или сжиматься. В этом случае из возрастания энтропии не следует стремления системы к термодинамического равновесию и парадокс «тепловой смерти» Вселенной не возникает.
Критика теории «тепловой смерти» Вселенной основывается в основном на утверждении, что, несмотря на логичность аргументов, тепловая смерть все еще не наступила (т. н. в космологии «термодинамический парадокс»).
В любом случае знания о Вселенной еще ничтожно малы, поэтому любые прогнозы относительно будущего Вселенной остаются лишь догадками. Например, в соответствии с современными физическими представлениями мы можем говорить лишь о наблюдаемой части Вселенной. На данном этапе человечество не имеет возможности доказать ни то, что Вселенная есть замкнутая система, ни обратное.
Флуктуации и второй закон термодинамики
В системах, состоящих из сравнительно небольшого числа частиц, наблюдаются значительные флуктуации, представляющие собой отклонения от второго начала термодинамики.
Флуктуацией физической величины L, характеризующей систему, называется отклонение истинного значения величины L от её среднего значения < L>, обусловленное хаотическим тепловым движением частиц системы.
В флуктуационных колебаниях наблюдаются процессы, в которых система переходит от более вероятного состояния к менее вероятному состоянию, т.е. энтропия уменьшается. Примером служит броуновское движение. В этих опытах мы наблюдаем флуктуации давления в небольшом объёме, приходящемся на частицу.
В случае большого числа частиц флуктуации незначительны. Так, температура 1мг воды, находящейся при комнатной температуре в равновесии будет испытывать колебания  10-8 градуса.
10-8 градуса.
Реальные газы
Реальный газ – газ, свойства которого (в отличие от идеального газа) зависит от взаимодействия молекул.
Свойства этих газов резко отличаются при высоких давлениях и низких температурах, когда начинают проявляться квантовые эффекты.
Силы и потенциальная энергия межмолекулярного взаимодействия
Модель идеального газа, используемая в молекулярно-кинетической теории газов, позволяет описывать поведение разреженных реальных газов при достаточно высоких температурах и низких давлениях. При выводе уравнения состояния идеального газа размерами молекул и их взаимодействием друг с другом пренебрегают. Повышение давления приводит к уменьшению среднего расстояния между молекулами, поэтому необходимо учитывать объем молекул и взаимодействие между ними. Taк, в 1 м3 газа при нормальных условиях содержится 2,68×1025 молекул, занимающих объем примерно 10–4 м3 (радиус молекулы примерно 10–10 м), которым по сравнению с объемом газа (1 м3) можно пренебречь. При давлении 500 Мпа (1 атм = 101,3 кПа) объем молекул составит уже половину всего объема газа. Таким образом, при высоких давлениях и низких температурах указанная модель идеального газа непригодна.
При рассмотренииреальных газов — газов, свойства которых зависят от взаимодействия молекул, надо учитыватьсилы межмолекулярного взаимодействия. Они проявляются на расстояниях r 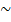 10–9 м и быстро убывают при увеличении расстояния между молекулами. Такие силы называютсякороткодействующими.
10–9 м и быстро убывают при увеличении расстояния между молекулами. Такие силы называютсякороткодействующими.
Межмолекулярные взаимодействия - взаимодействия молекул между собой, не приводящее к разрыву или образованию новых химических связей. Межмолекулярные взаимодействия определяют отличие реальных газов от идеальных, существование жидкостей и молекулярных кристаллов. От межмолекулярных взаимодействий зависят многие структурные, спектральные, термодинамические, теплофизические и другие свойства веществ.
Основу межмолекулярных взаимодействий составляют кулоновские силы взаимодействия между электронами и ядрами одной молекулы и ядрами и электронами другой.
По мере развития представлений о строении атома и квантовой механики, было выяснено, что между молекулами вещества одновременно действуютсилы притяжения и силы отталкивания. На рис. 134 a приведена качественная зависимость сил межмолекулярного взаимодействия от расстояния r между молекулами, где Fо и Fп — соответственно силы отталкивания и притяжения, a F —их результирующая. Силы отталкивания считаются положительными, а силы взаимного притяжения — отрицательными.

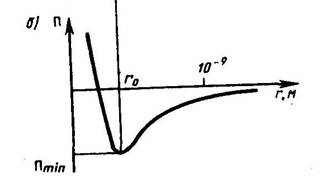
Рис. 134.
На расстоянии r = r0 результирующая сила F = 0, т.е. силы притяжения и отталкивания уравновешивают друг друга. Таким образом, расстояние r0 соответствует равновесному расстоянию между молекулами, на котором бы они находились в отсутствие теплового движения. При r < r0 преобладают силы отталкивания (F>0), при r > r0 — силы притяжения (F<0). На расстояниях r > 10–9 м межмолекулярные силы взаимодействия практически отсутствуют (F = 0).
Элементарная работа  A силы F при увеличении расстояния между молекулами на dr совершается за счет уменьшения взаимной потенциальной энергии молекул, т. е.
A силы F при увеличении расстояния между молекулами на dr совершается за счет уменьшения взаимной потенциальной энергии молекул, т. е.
 A = F dr = - dП,(1)
A = F dr = - dП,(1)
где П – потенциальная энергия межмолекулярного взаимодействия.
Из анализа качественной зависимости потенциальной энергии взаимодействия молекул от расстояния между ними (рис. 134, б) следует, что если молекулы находятся друг от друга на расстоянии, на котором межмолекулярные силы взаимодействия не действуют (r 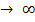 ), то П=0. При постепенном сближении молекул между, ними появляются силы притяжения (F<0), которые совершают положительную работу (
), то П=0. При постепенном сближении молекул между, ними появляются силы притяжения (F<0), которые совершают положительную работу (  = Fdr>0).Тогда, согласно (1), потенциальная энергия взаимодействия уменьшается, достигая минимума при r = r0. При r < r0 с уменьшением r силы отталкивания (F>0) резко возрастают и совершаемая против них работа отрицательна (
= Fdr>0).Тогда, согласно (1), потенциальная энергия взаимодействия уменьшается, достигая минимума при r = r0. При r < r0 с уменьшением r силы отталкивания (F>0) резко возрастают и совершаемая против них работа отрицательна (  A=Fdr <0). Потенциальная энергия начинает тоже резко возрастать и становится положительной. Из данной потенциальной кривой следует, что система из двух взаимодействующих молекул в состоянии устойчивого равновесия (r = r0) обладает минимальной аннцииальной энергией.
A=Fdr <0). Потенциальная энергия начинает тоже резко возрастать и становится положительной. Из данной потенциальной кривой следует, что система из двух взаимодействующих молекул в состоянии устойчивого равновесия (r = r0) обладает минимальной аннцииальной энергией.
Критерием различных агрегатных состояний вещества является соотношениемежду величинами Пmin и kT. Пmin — наименьшая потенциальная энергия взаимодействия молекул — определяет работу, которую нужно совершить против сил притяжения для того, чтобы разъединить молекулы, находящиеся в равновесии (r = r0); kT определяет удвоенную среднюю энергию, приходящуюся на одну степень свободы хаотического (теплового) движения молекул. Возможны следующие случаи:
- Пmin<<kT – вещество находиться в газообразном состоянии, так как интенсивное тепловое движение молекул препятствует соединению молекул;
- Пmin<<kT – вещество находится в твёрдом состоянии, так как молекулы, притягиваясь друг к другу, не могут удалиться на значительные расстояния и колеблются около положений равновесия, определяемого расстоянием r0;
- Пmin  – вещество находится в жидком состоянии, так как в результате теплового движения молекулы перемещаются в пространстве, обмениваясь местами, но не расходясь на расстояние, превышающее r0.
– вещество находится в жидком состоянии, так как в результате теплового движения молекулы перемещаются в пространстве, обмениваясь местами, но не расходясь на расстояние, превышающее r0.
Таким образом, любое вещество в зависимости от температуры может находиться в газообразном, жидком или твердом агрегатном состоянии, причем температура перехода из одного агрегатного состояния в другое зависит от значения Пmin, для данного вещества. Например, у инертных газов Пmin мало, а у металлов велико, поэтому при обычных (комнатных) температурах они находятся соответственно в газообразном и твердом состояниях.
Уравнение Ван – дер – Ваальса[49]
Для реальных газов необходимо учитывать размеры молекул и их взаимодействие друг с другом, поэтому модель идеального газа и уравнение Клапейрона – Менделеева (для моля газа) P  = RT, описывающее идеальный газ, для реальных газов непригодно.
= RT, описывающее идеальный газ, для реальных газов непригодно.
Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, голландский физик И. Ван-дер-Ваальс (1837—1923) вывел уравнение состояния реального газа. Ван-дер-Ваальсом в уравнение Клапейрона — Менделеева введены две поправки.
1). Учет собственного объема молекул. Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не 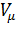 , а
, а 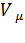 — b, где b — объем,занимаемый самими молекулами,
— b, где b — объем,занимаемый самими молекулами, 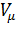 – молярный объём.
– молярный объём.
Объем b равен учетверенному собственному объему молекул. Если, например, в сосуде находятся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние, меньшее диаметра d молекулы. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса d, т. е. объем, равный восьми объемам молекулы или учетверенному объему молекулы в расчете на одну молекулу.
2). Учет притяжения молекул. Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислениям Ван-дер-Ваальса. Так как сила, действующая на каждую молекулу со стороны остальных, пропорциональна числу окружающих молекул, т.е. плотности газа, то и  будет пропорциональна квадрату плотности газа или обратно пропорциональна квадрату объёма:. P′ =
будет пропорциональна квадрату плотности газа или обратно пропорциональна квадрату объёма:. P′ =  , где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения,
, где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения, 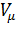 — молярный объем.
— молярный объем.
Вводя эти поправки, получимуравнение Ван-дер-Ваальса для моля газа(уравнение состояния реальных газов): (P +  ) (
) ( 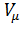 – b) = RT.
– b) = RT.
Для произвольного количества вещества v газа (v =  ) с учетом того, что V=v
) с учетом того, что V=v 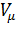 уравнение Ван-дер-Ваальса примет вид: (P +
уравнение Ван-дер-Ваальса примет вид: (P +  ) (
) ( 
 b) = RT) или
b) = RT) или
(P +  ) (V
) (V  b) =
b) =  RT,
RT,
где поправки а и b — постоянные для каждого газа величины, определяемые опытным путем.
В СИ: [a] =  ; [b] =
; [b] =  .
.
Для нахождения критических параметров подставим их значения в уравнение Ван – дер – Ваальса и запишем: РкV3  (RTк + Ркb)V2 + aV
(RTк + Ркb)V2 + aV  ab = 0. (1)
ab = 0. (1)
Поскольку в критической точке все три корня совпадают и равны Vк уравнение приводится к виду: Рк(V  Vк)3 = 0, (2)
Vк)3 = 0, (2)
или РкV3  3РкVкV2 + 3Рк
3РкVкV2 + 3Рк 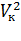 V
V  РкVк = 0.
РкVк = 0.
Taк как уравнения (1) и (2) тождественны, то в них должны быть равны и коэффициенты при неизвестных соответствующих степеней. Поэтому можно записать:
Рк 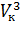 = ab; 3Рк
= ab; 3Рк 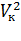 = a; 3Рк
= a; 3Рк  = RTк + Ркb. (3)
= RTк + Ркb. (3)
Решая полученные уравнения, найдем: 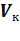 = 3b; Рк =
= 3b; Рк =  ; Tк =
; Tк = 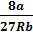 .
.
Уравнение Ван – дер – Вальса – уравнение третьей степени относительно V, следовательно, имеет три корня (два из которых могут быть комплексными), т.е. при постоянной температуре и определённом давлении у моля газа могут быть три различных объёма.
Реальные газы описываются уравнением Ван – дер – Ваальса лишь приближённо. В целом уравнение Ван – дер – Ваальса даёт лишь качественную картину реального газа. Существуют и другие уравнения, некоторые из них даже точнее описывают реальные газы, но не рассматриваются из-за их сложности.
Внутренняя энергия реального газа
Внутренняя энергия реального газа будем определяться суммой кинетической энергии K теплового движения его молекул и потенциальной энергии взаимодействия молекул между собой – П: U = К+П.
Кинетическая энергия поступательного и вращательного движений молекул определяет внутреннюю энергию идеального газа: 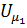 =
=  RT= CVT, где CV – молярная теплоёмкость газа при постоянном объёме.
RT= CVT, где CV – молярная теплоёмкость газа при постоянном объёме.
Работа  сил молекулярного сцепления, которые вызывают внутреннее давление
сил молекулярного сцепления, которые вызывают внутреннее давление  и изменение объёма dV:
и изменение объёма dV:  =
=  dV.
dV.
Так как  =
= 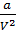 , то изменение потенциальной энергии, которое произошло за счёт совершения работы
, то изменение потенциальной энергии, которое произошло за счёт совершения работы  , равно: d
, равно: d  =
= 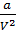 dV.
dV.
Интегрируя это выражение, получим:  =
= 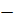
 + const.
+ const.
Const находится из условия, что расстояние между молекулами при безграничном увеличении объёма возрастают и потенциальную энергию при этом следует считать равной нулю: V  , то
, то 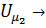 0 и const= 0.
0 и const= 0.
Для конечного объёма V потенциальная энергия моля газа равна:  =
= 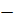
 .
.
Внутренняя энергия моля реального газа равна: 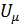 =
= 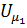 +
+  = CVT
= CVT 
 .
.
Таким образом, внутренняя энергия реального газа зависит от температуры T и объёма V:  = CVT
= CVT 
 . (1)
. (1)
Последнее уравнение справедливо для моля реального газа.
Из формулы для внутренней энергии реального газа следует, что его внутренняя энергия растет как с увеличением температуры, так и с увеличением объема. Если реальный газ будет расширяться или сжиматься адиабатически и без совершения внешней работы, то для него, согласно первому началу термодинамики:
ΔQ = ΔU + ΔA; ΔQ = 0, ΔA = 0; ⇒ ΔU = 0 → U = const,
и внутренняя энергия должна оставаться постоянной. Поэтому, из формулы (1) для реального газа, совершающего адиабатический переход без совершения работы, можно записать: T1 – T2 = ( 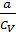 )[(
)[( 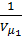 ) – (
) – ( 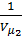 )] .
)] .
Из этого уравнения следует, что изменение объема и изменение температуры имеют разные знаки. Следовательно, при адиабатическом расширении в вакуум, реальный газ должен охлаждаться, а при сжатии – нагреваться.
Отметим, что для идеального газа этот эффект не наблюдается:
ΔU = CvΔT = 0 → ΔT = 0 → T = const.
Рассмотрим расширение реального газа в пустоту. В этом случае внешнее давление равно нулю, поэтому газ не совершает работу против внешних сил. Но в реальном газе действуют силы межмолекулярного взаимодействия, и при расширении газа совершается работа по преодолению этих сил за счет внутренней энергии газа. Вследствие этого температура реального газа при расширении в пустоту должна понижаться.
Однако это не совсем так. В некоторых случаях может происходить и повышение температуры. Реальный газ при расширении охлаждается в том случае, когда преобладает действие сил притяжения между молекулами газа. Тогда молекулы газа совершают работу против сил притяжения за счет своей кинетической энергии, вследствие чего кинетическая энергия уменьшается, т.е. температура понижается. Если преобладает действие сил отталкивания между молекулами газа, то при расширении скорость молекул не уменьшается, а увеличивается, т.е. температура возрастает.
Следовательно, в зависимости от того, что преобладает — силы притяжения между молекулами или силы отталкивания, — может получиться при расширении газа в пустоту или нагревание газа, или охлаждение.
Изменение внутренней энергии реального газа при расширении положено в основу принципа действия машины для сжижения газов.
Изотермы Ван – дер - Ваальса
Для исследования поведения реального газа рассмотримизотермы Ван-дер-Ваальса — кривые зависимости Р от  при заданных Т, определяемые уравнением Ван-дер-Ваальса для моля газа. Эти кривые (рассматриваются для четырех различных температур; рис. 135) имеют довольно своеобразный характер. При высоких температурах (T > Tк) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре Tк на изотерме имеется лишь одна точка перегиба К.
при заданных Т, определяемые уравнением Ван-дер-Ваальса для моля газа. Эти кривые (рассматриваются для четырех различных температур; рис. 135) имеют довольно своеобразный характер. При высоких температурах (T > Tк) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре Tк на изотерме имеется лишь одна точка перегиба К.
Эта изотерма называется критической, соответствующая ей температура Tк — критической температурой; точка перегиба К называется критической точкой; в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объемVк, и давление Ркназываются также критическими. Состояние с критическими параметрами (Рк, Vк, Tк) называется критическим состоянием. При низких температурах (Т < Tк ) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.
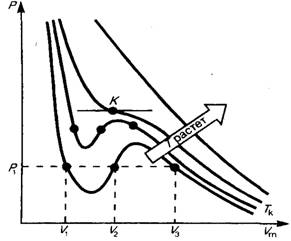
Рис. 135.
При T  Tк стирается различие между жидким и газообразным состоянием вещества, различие в плотности жидкости и пара, обращаются в нуль удельная теплота парообразования и коэффициент поверхностного натяжения (рис. 136).
Tк стирается различие между жидким и газообразным состоянием вещества, различие в плотности жидкости и пара, обращаются в нуль удельная теплота парообразования и коэффициент поверхностного натяжения (рис. 136).
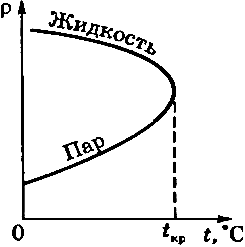
Рис. 136.
Для пояснения характера изотерм преобразуем уравнение Ван-дер-Ваальса к виду: P  (RT + Pb)
(RT + Pb)  + a
+ a 
 ab = 0.
ab = 0.
Уравнение Ван – дер – Ваальса при заданных P и Т является уравнением третьей степени относительно  ; следовательно, оно может иметь либо три вещественных корня, либо один вещественный и два мнимых, причем физический смысл имеют лишь вещественные положительные корни. Поэтому первому случаю соответствуют изотермы при низких температурах (три значения объема газа V1, V2 и V3 отвечают (символ «
; следовательно, оно может иметь либо три вещественных корня, либо один вещественный и два мнимых, причем физический смысл имеют лишь вещественные положительные корни. Поэтому первому случаю соответствуют изотермы при низких температурах (три значения объема газа V1, V2 и V3 отвечают (символ «  » для простоты опускаем) одному значению давления P1, второму случаю — изотермы при высоких температурах.
» для простоты опускаем) одному значению давления P1, второму случаю — изотермы при высоких температурах.
Рассматривая различные участки изотермы при T<Тк (рис. 137), видим, что на участках 1—3 и 5—7 при уменьшении объема  давление Р возрастает, что естественно. На участке 3—5 сжатие вещества приводит к уменьшению давления; практика же показывает, что такие состояния в природе не осуществляются. Наличие участка 3—5 означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды; в некоторый момент должно наступить скачкообразное изменение состояния и распад вещества на две фазы. Таким образом, истинная изотерма будет иметь вид ломаной линии 7—6—2—1. Часть 6–7 отвечает газообразному состоянию, а часть 2–1 — жидкому. В состояниях, соответствующих горизонтальному участку изотермы 6—2, наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным.
давление Р возрастает, что естественно. На участке 3—5 сжатие вещества приводит к уменьшению давления; практика же показывает, что такие состояния в природе не осуществляются. Наличие участка 3—5 означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды; в некоторый момент должно наступить скачкообразное изменение состояния и распад вещества на две фазы. Таким образом, истинная изотерма будет иметь вид ломаной линии 7—6—2—1. Часть 6–7 отвечает газообразному состоянию, а часть 2–1 — жидкому. В состояниях, соответствующих горизонтальному участку изотермы 6—2, наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным.
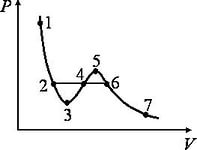
Рис. 137.
Данные выводы, следующие из анализа уравнения Ван-дер-Ваальса, были подтверждены опытами ирландского ученого Т. Эндрюса (1813—1885), изучавшего изотермическое сжатие углекислого газа. Отличие экспериментальных (Эндрюс) и теоретических (Ван-дер-Ваальс) изотерм заключается в том, что превращению газа в жидкость в первом случае соответствуют горизонтальные участки, а во втором — волнообразные.
Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая (рис. 138), ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму Р,  под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар), слева от нее находится область жидкого состояния, а справа — область пара. Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращен в жидкость ни при каком давлении.
под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар), слева от нее находится область жидкого состояния, а справа — область пара. Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращен в жидкость ни при каком давлении.
Сравнивая изотерму Ван-дер-Ваальса с изотермой Эндрюса (верхняя кривая на рис. 138), видим, что последняя имеет прямолинейный участок 2—6, соответствующий двухфазным состояниям вещества. Правда, при некоторых условиях могут быть реализованы состояния, изображаемые участками анн-дер-ваальсовой изотермы 5—6 и 2—3. Эти неустойчивые состояния называютсяметастабильными[50]. Участок 2—3 изображаетперегретую жидкость, 5—6 — пересыщенный пар. Обе фазы ограниченно устойчивы.

Рис. 138.
При достаточно низких температурах изотерма пересекает ось  , переходя в область отрицательных давлений (нижняя кривая на рис. 139). Вещество под отрицательным давлением находится в состоянии растяжения. При некоторых условиях такие состояния также реализуются. Участок 8—9 на нижней изотерме соответствует перегретой жидкости, участок 9—10 — растянутой жидкости.
, переходя в область отрицательных давлений (нижняя кривая на рис. 139). Вещество под отрицательным давлением находится в состоянии растяжения. При некоторых условиях такие состояния также реализуются. Участок 8—9 на нижней изотерме соответствует перегретой жидкости, участок 9—10 — растянутой жидкости.
Для нахождения критических параметров подставим их значения в уравнение Ван – дер – Ваальса и запишем: РкV3  (RTк + Ркb)V2 + aV
(RTк + Ркb)V2 + aV  ab = 0. (1)
ab = 0. (1)
Поскольку в критической точке все три корня совпадают и равны Vк уравнение приводится к виду: Рк(V  Vк)3 = 0, или РкV3
Vк)3 = 0, или РкV3  3РкVкV2 + 3Рк
3РкVкV2 + 3Рк 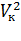 V
V  РкVк = 0. (2)
РкVк = 0. (2)
Taк как уравнения (1) и (2) тождественны, то в них должны быть равны и коэффициенты при неизвестных соответствующих степеней. Поэтому можно записать:
Рк 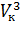 = ab; 3Рк
= ab; 3Рк 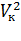 = a; 3Рк
= a; 3Рк  = RTк + Ркb. (3)
= RTк + Ркb. (3)
Решая полученные уравнения, найдем: 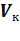 = 3b; Рк =
= 3b; Рк =  ; Tк =
; Tк = 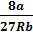 .
.
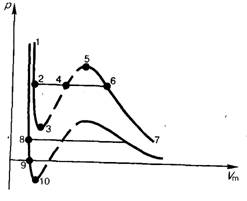
Рис. 139.
Эффект Джоуля – Томсона
Наличие потенциальной энергии взаимодействия молекул проявляется в эффекте Джоуля – Томсона: изменение температуры реального газа при изменении его объёма без теплообмена и без совершения внешней работы.
Если температура Т газа понижается (∆Т<0), то эффект считается положительным; если газ нагревается ((∆Т> 0), то эффект считается отрицательным. Если при расширении не нагревается и не охлаждается, то эффект Джоуля – Томсона равен нулю. Такое состояние отображается точкой инверсии. Точка инверсии определяет температуру, вблизи которой эффект меняет свой знак.
Положительный эффект Джоуля – Томсона используется при получении низких температур.
Глубокого охлаждения газов достигают двумя путями:
1). Температура газа понижается при его расширении вследствие совершения работы против сил сцепления молекул;
2). Температура газа понижается при адиабатном расширении вследствие совершения работы против внешних сил.
Применение первого способа возможно при охлаждении газа ниже температуры инверсии и ниже критической температуры. В настоящее время подвергнуты сжижению и отвердеванию все газы, включая гелий, критическая температура которого ТК = 5 К.
Жидкости
Жи́дкость — вещество, находящееся в жидком агрегатном состоянии, занимающем промежуточное положение между твёрдым и газообразным состояниями. Основным свойством жидкости, отличающим её от веществ, находящихся в других агрегатных состояниях, является способность неограниченно менять форму под действием касательных механических напряжений, даже сколь угодно малых, практически сохраняя при этом объём.
Общая информация о жидком солстоянии
Жидкое состояние обычно считают промежуточным между твёрдым телом и газом: газ не сохраняет ни объём, ни форму, а твёрдое тело сохраняет и то, и другое.
Форма жидких тел может полностью или отчасти определяться тем, что их поверхность ведёт себя как упругая мембрана. Так, вода может собираться в капли. Но жидкость способна течь даже под своей неподвижной поверхностью, и это тоже означает несохранение формы (внутренних частей жидкого тела).
Молекулы жидкости не имеют определённого положения, но в то же время им недоступна полная свобода перемещений. Между ними существует притяжение, достаточно сильное, чтобы удержать их на близком расстоянии.
Вещество в жидком состоянии существует в определённом интервале температур, ниже которого переходит в твердое состояние (происходит кристаллизация либо превращение в твердотельное аморфное состояние — стекло), выше — в газообразное (происходит испарение). Границы этого интервала зависят от давления.
Как правило, вещество в жидком состоянии имеет только одну модификацию. (Наиболее важные исключения — это квантовые жидкости и жидкие кристаллы.) Поэтому в большинстве случаев жидкость является не только агрегатным состоянием, но и термодинамической фазой (жидкая фаза).
Все жидкости принято делить на чистые жидкости и смеси. Некоторые смеси жидкостей имеют большое значение для жизни: кровь, морская вода и др. Жидкости могут выполнять функцию растворителей.
Физические свойства жидкостей
1).Текучесть
Основным свойством жидкостей является текучесть. Если к участку жидкости, находящейся в равновесии, приложить внешнюю силу, то возникает поток частиц жидкости в том направлении, в котором эта сила приложена: жидкость течёт. Таким образом, под действием неуравновешенных внешних сил жидкость не сохраняет форму и относительное расположение частей, и поэтому принимает форму сосуда, в котором находится.
В отличие от пластичных твёрдых тел, жидкость не имеет предела текучести: достаточно приложить сколь угодно малую внешнюю силу, чтобы жидкость потекла.
2).Сохранение объёма
Одним из характерных свойств жидкости является то, что она имеет определённый объём (при неизменных внешних условиях). Жидкость чрезвычайно трудно сжать механически, поскольку, в отличие от газа, между молекулами очень мало свободного пространства. Давление, производимое на жидкость, заключенную в сосуд, передаётся без изменения в каждую точку объёма этой жидкости (закон Паскаля, справедлив также и для газов). Эта особенность, наряду с очень малой сжимаемостью, используется в гидравлических машинах.
Жидкости обычно увеличивают объём (расширяются) при нагревании и уменьшают объём (сжимаются) при охлаждении. Впрочем, встречаются и исключения, например, вода сжимается при нагревании, при нормальном давлении и температуре от 0 °C до приблизительно 4 °C.
3).Вязкость
Кроме того, жидкости (как и газы) характеризуются вязкостью. Она определяется как способность оказывать сопротивление перемещению одной из частей относительно другой — то есть как внутреннее трение.
Когда соседние слои жидкости движутся относительно друг друга, неизбежно происходит столкновение молекул дополнительно к тому, которое обусловлено тепловым движением. Возникают силы, затормаживающие упорядоченное движение. При этом кинетическая энергия упорядоченного движения переходит в тепловую — энергию хаотического движения молекул.
Жидкость в сосуде, приведённая в движение и предоставленная самой себе, постепенно остановится, но её температура повысится.
4).Смешиваемость
Смешиваемость — способность жидкостей растворяться друг в друге. Пример смешиваемых жидкостей: вода и этиловый спирт, пример несмешиваемых: вода и жидкое масло.
5). Образование свободной поверхности и поверхностное натяжение
Из-за сохранения объёма жидкость способна образовывать свободную поверхность. Такая поверхность является поверхностью раздела фаз данного вещества: по одну сторону находится жидкая фаза, по другую — газообразная (пар), и, возможно, другие газы, например, воздух.
Если жидкая и газообразная фазы одного и того же вещества соприкасаются, возникают силы, которые стремятся уменьшить площадь поверхности раздела — силы поверхностного натяжения. Поверхность раздела ведёт себя как упругая мембрана, которая стремится стянуться.
6).Волны плотности
Хотя жидкость чрезвычайно трудно сжать, тем не менее, при изменении давления её объем и плотность всё же меняются. Это происходит не мгновенно; так, если сжимается один участок, то на другие участки такое сжатие передаётся с запаздыванием. Это означает, что внутри жидкости способны распространяться упругие волны, более конкретно, волны плотности. Вместе с плотностью меняются и другие физические величины, например, температура.
Если при распространении волны́ плотность меняется достаточно слабо, такая волна называется звуковой волной, или звуком.
Если плотность меняется достаточно сильно, то такая волна называется ударной волной. Ударная волна описывается другими уравнениями.
Волны плотности в жидкости являются продольными, то есть плотность меняется вдоль направления распространения волны. Поперечные упругие волны в жидкости отсутствуют из-за несохранения формы.
Упругие волны в жидкости со временем затухают, их энергия постепенно переходит в тепловую энергию. Причины затухания — вязкость, «классическое поглощение», молекулярная релаксация и другие. При этом работает так называемая вторая, или объёмная вязкость — внутреннее трение при изменении плотности. Ударная волна в результате затухания через какое-то время переходит в звуковую.
Упругие волны в жидкости подвержены также рассеянию на неоднородностях, возникающих в результате хаотического теплового движения молекул.
Строение жидкостей
Экспериментальные исследования жидкого состояния вещества, основанные на наблюдении дифракции рентгеновских лучей и потоков нейтронов при прохождении их через жидкие среды, обнаружили наличие в жидкости ближнего порядка[51], т.е. наличие некоторой упорядоченности в расположении частиц лишь на малом расстоянии от какой-либо выделенной позиции (рис. 140).
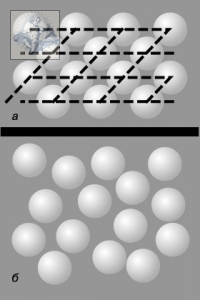
Рис. 140. Дальний и ближний порядок : а – двумерная модель твердого тела, иллюстрирующая наличие дальнего порядка; б – двумерная модель жидкости, иллюстрирующая наличие только ближнего порядка.
Взаимное расположение соседних частиц в жидкостях сходно с упорядоченным расположением соседних частиц в кристаллах. Однако, эта упорядоченность в жидкостях наблюдается лишь внутри малых объёмов. При расстояниях r > (3  4) d от некоторой выбранной «центральной» молекулы упорядоченность нарушается (d- эффективный диаметр молекулы). Подобная упорядоченность в расположении частиц в жидкостях и называется ближним порядком.
4) d от некоторой выбранной «центральной» молекулы упорядоченность нарушается (d- эффективный диаметр молекулы). Подобная упорядоченность в расположении частиц в жидкостях и называется ближним порядком.
Из – за отсутствия дальнего порядка жидкости, за немногим исключением, не обнаруживают анизотропии, характерной для кристаллов. По этой причине структуру жидкости иногда называют квазикристаллической или кристаллоподобной.
Впервые идея о близости некоторых свойств жидкостей (особенно расплавов металлов) и кристаллических твердых тел была высказана и затем развивалась в работах советского физика Я.И.Френкеля еще 1930–1940-х. Согласно взглядам Френкеля, получившим теперь всеобщее признание, тепловое движение атомов и молекул в жидкости состоит из нерегулярных колебаний со средней частотой, близкой к частоте колебаний атомов в кристаллических телах. Центр колебаний определяется при этом полем сил соседних частиц и смещается вместе со смещениями этих частиц.
Упрощенно можно представить такое тепловое движение как наложение друг на друга сравнительно редких перескоков частиц из одних временных положений равновесия в другие и тепловых колебаний в промежутках между скачками. Среднее время <  > «оседлого» пребывания молекулы жидкости вблизи некотрого положения равновесия называется временем релаксации. По истечеии времени <
> «оседлого» пребывания молекулы жидкости вблизи некотрого положения равновесия называется временем релаксации. По истечеии времени <  > молекула меняет место равновесия, скачком перемещаясь в новое положение, отстоящее от предыдущего на расстояние порядка размеров самих молекул. Таким образом, молекула медленно перемещается внутри жидкости. С ростом температуры время <
> молекула меняет место равновесия, скачком перемещаясь в новое положение, отстоящее от предыдущего на расстояние порядка размеров самих молекул. Таким образом, молекула медленно перемещается внутри жидкости. С ростом температуры время <  > уменьшается, подвиждность молекул возрасчтает, что влечёт за собой уменьшенине вязкости жидкостей (возрастает текучесть). По образному выражению Я.И.Френкеля, молекулы странствуют по всему объему жидкости, ведя кочевой образ жизни, при котором кратковременные переезды сменяются относительно длинными периодами оседлой жизни.
> уменьшается, подвиждность молекул возрасчтает, что влечёт за собой уменьшенине вязкости жидкостей (возрастает текучесть). По образному выражению Я.И.Френкеля, молекулы странствуют по всему объему жидкости, ведя кочевой образ жизни, при котором кратковременные переезды сменяются относительно длинными периодами оседлой жизни.
Аморфные твёрдые тела (стекло, смолы, битум и т.д.) можно рассматривать как переохлаждённые жидкости, частицы которых из-за сильно возросшей вязкости имеют ограниченную подвижность.
Из-за малой упорядоченности жидкого состояния теория жидкости оказывается менее развитой, чем теория газов и кристаллических твердых тел. Пока нет полной теории жидкости.
Особый тип жидкостей – это некоторые органические соединения, состоящие из молекул удлиненной или дискообразной формы, или так называемые жидкие кристаллы. Взаимодействие между молекулами в таких жидкостях стремится выстроить длинные оси молекул в определенном порядке. При высоких температурах тепловое движение препятствует этому, и вещество представляет собой обычную жидкость. При температурах ниже критической в жидкости появляется выделенное направление, возникает дальний ориентационный порядок. Сохраняя основные черты жидкости, например, текучесть, жидкие кристаллы обладают характерными свойствами твердых кристаллов – анизотропией магнитных, электрических и оптических свойств. Эти их свойства (наряду с текучестью) находят многочисленные технические применения, например в электронных часах, калькуляторах, мобильных телефонах, а также в мониторах персональных компьютеров, телевизорах, в качестве индикаторов, табло и экранов для отображения цифровой, буквенной и аналоговой информации.
Поверхностное натяжение
Наиболее интересной особенностью жидкостей является наличие свободной поверхности. С поверхностью жидкости связана свободная энергия, пропорциональная площади S свободной поверхности жидкости: Есв..= 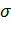 S. Так как свободная энергия изолированной системы стремится к минимуму, то жидкость (в отсутствие внешних полей) стремится принять форму, имеющую минимальную площадь поверхности. Таким образом, задача о форме жидкости сводится к изопериметрической задаче при заданных дополнительных условиях (начальное распределение, объём и т. п.). Свободная капля принимает форму шара, однако при более сложных условиях задача о форме поверхности жидкости становится исключительно сложной.
S. Так как свободная энергия изолированной системы стремится к минимуму, то жидкость (в отсутствие внешних полей) стремится принять форму, имеющую минимальную площадь поверхности. Таким образом, задача о форме жидкости сводится к изопериметрической задаче при заданных дополнительных условиях (начальное распределение, объём и т. п.). Свободная капля принимает форму шара, однако при более сложных условиях задача о форме поверхности жидкости становится исключительно сложной.
Жидкость, в отличие от газов, не заполняет весь объем сосуда, в который она налита. Между жидкостью и газом (или паром) образуется граница раздела, которая находится в особых условиях по сравнению с остальной массой жидкости. Молекулы в пограничном слое жидкости, в отличие от молекул в ее глубине, окружены другими молекулами той же жидкости не со всех сторон. Силы межмолекулярного взаимодействия, действующие на одну из молекул внутри жидкости со стороны соседних молекул, в среднем взаимно скомпенсированы (рис. 141).

Рис. 141.
Любая молекула в пограничном слое притягивается молекулами, находящимися внутри жидкости (силами, действующими на данную молекулу жидкости со стороны молекул газа (или пара) можно пренебречь. В результате появляется некоторая равнодействующая сила, направленная вглубь жидкости. Поверхностные молекулы силами межмолекулярного притяжения втягиваются внутрь жидкости (рис. 142).

Рис. 142.
Но все молекулы, в том числе и молекулы пограничного слоя, должны находиться в состоянии равновесия. Это равновесие достигается за счет некоторого уменьшения расстояния между молекулами поверхностного слоя и их ближайшими соседями внутри жидкости. При уменьшении расстояния между молекулами возникают силы отталкивания. Молекулы поверхностного слоя упакованы несколько более плотно, а поэтому они обладают дополнительным запасом потенциальной энергии по сравнению с внутренними молекулами. Следовательно, молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами внутри жидкости потенциальной энергией П, равной свободной энергии Есв.. Таким образом, потенциальная энергия поверхности жидкости пропорциональна ее площади: П =  S.
S.
Из механики известно, что равновесным состояниям системы соответствует минимальное значение ее потенциальной энергии, т.е. свободная поверхность жидкости стремится сократить свою площадь. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, сокращающие (стягивающие) эту поверхность. Эти силы 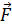 i называются силами поверхностного натяжения.
i называются силами поверхностного натяжения.
Выберем на поверхности жидкости некоторый замкнутый контур L. Для всех молекул, лежащих внутри этого контура, все силы 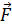 i, взаимно уравновешиваются. Однако для молекул, расположенных вдоль контура L, силы
i, взаимно уравновешиваются. Однако для молекул, расположенных вдоль контура L, силы 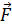 i направлены наружу, являются внешними силами; они перпендикулярны периметру и касательные к поверхности жидкости. Эти силы, растягивающие плёнку, и являются силами поверхностного натяжения (рис. 143).
i направлены наружу, являются внешними силами; они перпендикулярны периметру и касательные к поверхности жидкости. Эти силы, растягивающие плёнку, и являются силами поверхностного натяжения (рис. 143).

Рис. 143.
Сила поверхностного натяжения направлена по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует и пропорциональна длине этого участка:  i =
i = 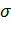 l.
l.
Наличие сил поверхностного натяжения делает поверхность жидкости похожей на упругую растянутую пленку, с той только разницей, что упругие силы в пленке зависят от площади ее поверхности (т. е. от того, как пленка деформирована), а силы поверхностного натяжения не зависят от площади поверхности жидкости.
Поверхностное натяжение – стремление жидкости уменьшить избыток своей потенциальной энергии на границе раздела с другой фазой (поверхностную энергию).
Таким образом, поверхностное натяжение имеет двойной физический смысл — энергетический (термодинамический) и силовой (механический). Энергетическое (термодинамическое) определение: поверхностное натяжение — это удельная работа увеличения поверхности при её растяжении при условии постоянства температуры. Силовое (механическое) определение: поверхностное натяжение — это сила, действующая на единицу длины линии, которая ограничивает поверхность жидкости.
Следует иметь в виду, что вследствие крайне низкой сжимаемости наличие более плотно упакованного поверхностного слоя не приводит к сколь-нибудь заметному изменению объема жидкости. Если молекула переместится с поверхности внутрь жидкости, силы межмолекулярного взаимодействия совершат положительную работу. Наоборот, чтобы вытащить некоторое количество молекул из глубины жидкости на поверхность (т. е. увеличить площадь поверхности жидкости), внешние силы должны совершить положительную работу ΔAвнеш. = П, пропорциональную изменению ΔS площади поверхности: ∆Авнешн.=  ∆S, где ∆S, где 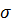 называется коэффициентомповерхностного натяжения (σ > 0).
Таким образом, с точки зрения энергетической: коэффициент поверхностного натяжения равен работе, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу: называется коэффициентомповерхностного натяжения (σ > 0).
Таким образом, с точки зрения энергетической: коэффициент поверхностного натяжения равен работе, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу:  = =  , , 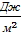 , с точки зрения силовой: коэффициентом поверхностного натяжения называется величина, численно равная силе поверхностного натяжения, приходящейся на единицу длины поверхности раздела сред: , с точки зрения силовой: коэффициентом поверхностного натяжения называется величина, численно равная силе поверхностного натяжения, приходящейся на единицу длины поверхности раздела сред:  = =  , ,  .
Коэффициент поверхностного натяжения зависит от химического состава жидкости и её температуры. С увеличением температуры .
Коэффициент поверхностного натяжения зависит от химического состава жидкости и её температуры. С увеличением температуры  уменьшается и обращается в нуль при критической температуре. При введении в жидкости примесей, поверхносто-активных веществ коэффициент поверхностного натяжения уменьшается.
Так как появление поверхности жидкости требует совершения работы, каждая среда «стремится» уменьшить площадь своей поверхности:
· в невесомости капля принимает сферическую форму (сфера имеет наименьшую площадь поверхности среди всех тел одинакового объёма).
· струя воды «слипается» в цилиндр.
· маленькие объекты с плотностью, большей плотности жидкости, способны «плавать» на поверхности жидкости, так как сила тяготения оказывается уравновешенной силой поверхностного натяжения.
· некоторые насекомые (например, водомерки) способны передвигаться по воде, удерживаясь на её поверхности за счёт сил поверхностного натяжения.
· На многих поверхностях, именуемых несмачиваемыми, вода (или другая жидкость) собирается в капли.
Обычно мы наблюдаем жидкости, подверженные действию сил земного тяготения. При этом жидкость принимает форму, соответствующую минимуму суммарной энергии – энергии в поле силы тяготения и поверхностной энергии.
Было доказано теоретически, что понятие поверхностного натяжения жидкости однозначно является частью понятия внутренней энергии.
Поверхностное натяжение может быть на границе газообразных, жидких и твёрдых тел. Обычно имеется в виду поверхностное натяжение жидких тел на границе «жидкость — газ». В случае жидкой поверхности раздела поверхностное натяжение правомерно также рассматривать как силу, действующую на единицу длины контура поверхности и стремящуюся сократить поверхность до минимума при заданных объёмах фаз. Прибор для измерения поверхностного натяжения называется тензиометром.
Пример. Некоторые жидкости, как, например, мыльная вода, обладают способностью образовывать тонкие пленки. Всем хорошо известные мыльные пузыри имеют правильную сферическую форму – в этом тоже проявляется действие сил поверхностного натяжения. Если в мыльный раствор опустить проволочную рамку, одна из сторон которой подвижна, то вся она затянется пленкой жидкости (рис. 144). уменьшается и обращается в нуль при критической температуре. При введении в жидкости примесей, поверхносто-активных веществ коэффициент поверхностного натяжения уменьшается.
Так как появление поверхности жидкости требует совершения работы, каждая среда «стремится» уменьшить площадь своей поверхности:
· в невесомости капля принимает сферическую форму (сфера имеет наименьшую площадь поверхности среди всех тел одинакового объёма).
· струя воды «слипается» в цилиндр.
· маленькие объекты с плотностью, большей плотности жидкости, способны «плавать» на поверхности жидкости, так как сила тяготения оказывается уравновешенной силой поверхностного натяжения.
· некоторые насекомые (например, водомерки) способны передвигаться по воде, удерживаясь на её поверхности за счёт сил поверхностного натяжения.
· На многих поверхностях, именуемых несмачиваемыми, вода (или другая жидкость) собирается в капли.
Обычно мы наблюдаем жидкости, подверженные действию сил земного тяготения. При этом жидкость принимает форму, соответствующую минимуму суммарной энергии – энергии в поле силы тяготения и поверхностной энергии.
Было доказано теоретически, что понятие поверхностного натяжения жидкости однозначно является частью понятия внутренней энергии.
Поверхностное натяжение может быть на границе газообразных, жидких и твёрдых тел. Обычно имеется в виду поверхностное натяжение жидких тел на границе «жидкость — газ». В случае жидкой поверхности раздела поверхностное натяжение правомерно также рассматривать как силу, действующую на единицу длины контура поверхности и стремящуюся сократить поверхность до минимума при заданных объёмах фаз. Прибор для измерения поверхностного натяжения называется тензиометром.
Пример. Некоторые жидкости, как, например, мыльная вода, обладают способностью образовывать тонкие пленки. Всем хорошо известные мыльные пузыри имеют правильную сферическую форму – в этом тоже проявляется действие сил поверхностного натяжения. Если в мыльный раствор опустить проволочную рамку, одна из сторон которой подвижна, то вся она затянется пленкой жидкости (рис. 144).
Силы поверхностного натяжения стремятся сократить поверхность пленки. Для равновесия подвижной стороны рамки к ней нужно приложить внешнюю силу:
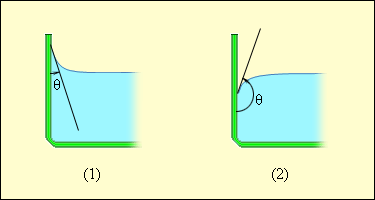
Если под действием силы Давление под изогнутой поверхностью жидкости. Формула Лапласа Известно, что поверхность жидкости около стенок сосуда искривляется. Свободная поверхность жидкости, искривлённая около стенок сосуда, называется мениском (рис. 145).
Рис. 145. Краевые углы смачивающей (1) и несмачивающей (2) жидкостей. Рассмотрим тонкую жидкую плёнку, толщиной которой можно пренебречь. Стремясь минимизировать свою свободную энергию, плёнка создаёт разность давления с разных сторон. Из-за действия сил поверхностного натяжения в каплях жидкости и внутри мыльных пузырей возникает добавочное давление ΔР (плёнка сжимается до тех пор, пока давление внутри пузыря не будет превышать атмосферное на величину добавочного давления плёнки ΔР). Рассмотрим поверхность жидкости, опирающуюся на некоторый плоский контур (рис.146, а). Если поверхность жидкости не плоская, то стремление ее к сокращению и приведет к возникновению давления ∆Р, дополнительного к тому, которое испытывает жидкость с плоской поверхностью. В случае выпуклой поверхности это дополнительное давление положительно (рис. 146, б), в случае вогнутой поверхности — отрицательно (рис. 146, в). В последнем случае поверхностный слой, стремясь сократиться, растягивает жидкость.
|
Рис. 146.
Величина добавочного давления, очевидно, должна возрастать с увеличением коэффициента поверхностного натяжения 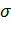 и кривизны поверхности R.
и кривизны поверхности R.
Вычислим добавочное давление для сферической поверхности жидкости. Для этого рассечем мысленно сферическую каплю жидкости диаметральной плоскостью на два полушария (рис. 147). Из-за поверхностного натяжения оба полушария притягиваются друг к другу с силой, равной: F = 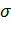 l = 2
l = 2  R
R 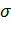 .
.
Эта сила прижимает друг к другу оба полушария по поверхности и, следовательно, обусловливает дополнительное давление: ∆P =  =
=  =
=  .
.
Кривизна сферической поверхности всюду одинакова и определяется радиусом сферы R. Очевидно, что чем меньше R, тем больше кривизна сферической поверхности.
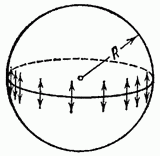
Рис. 147.
Избыточное давление внутри мыльного пузыря в два раза больше, так как пленка имеет две поверхности: ∆P =  .
.
Добавочное давление обусловливает изменение уровня жидкости в узких трубках (капиллярах), вследствие чего называется иногда капиллярным давлением.
Кривизну произвольной поверхности принято характеризовать так называемой средней кривизной <K>, которая может оказаться различной для разных точек поверхности[52].
Величина R дает кривизну сферы. В геометрии доказывается, что полусумма обратных радиусов кривизны для любой пары взаимно перпендикулярных нормальных сечений имеет одно и то же значение: <K>= 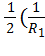 +
+  ). (1)
). (1)
Эта величина и есть средняя кривизна поверхности в данной точке. В этой формуле радиусы R1,2 — алгебраические величины. Если центр кривизны нормального сечения находится под данной поверхностью, соответствующий радиус кривизны положителен; если центр кривизны лежит над поверхностью, радиус кривизны отрицателен (рис.148).
Таким образом, неплоская поверхность может иметь среднюю кривизну, равную нулю. Для этого нужно, чтобы радиусы кривизны были одинаковы по величине и противоположны по знаку.
Например, для сферы центры кривизны в любой точке поверхности совпадают с центром сферы, поэтому R1 = R2 = R и ∆P = 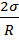 .Для случая поверхности кругового цилиндра радиуса R имеем: R1 = R; R2 =
.Для случая поверхности кругового цилиндра радиуса R имеем: R1 = R; R2 =  и ∆P =
и ∆P = 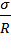 .
.
Можно доказать, что для поверхности любой формы справедливо соотношение: ∆P=2<K>. (2)
Подставив в формулу (2) выражение (1), получим формулу добавочного давления под произвольной поверхностью, называемую формулой Лапласа (рис. 148):
∆P = 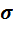 (
( 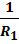 +
+  ).(3)
).(3)

Рис. 148.
Радиусы R1 и R2 в формуле (3) — алгебраические величины. Если центр кривизны нормального сечения находится под данной поверхностью, соответствующий радиус кривизны положителен; если центр кривизны лежит над поверхностью, радиус кривизны отрицателен.
Пример. Если в жидкости имеется пузырек газа, то поверхность пузырька, стремясь сократиться, будет ока
 Рис. 144.
Подвижная сторона проволочной рамки в равновесии под действием внешней силы
Рис. 144.
Подвижная сторона проволочной рамки в равновесии под действием внешней силы  н.
н. Δx = σ2LΔx
Δx = σ2LΔx  σ =
σ = 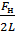 .
.