 |
|
Фазовые равновесия и превращения
Среди макроскопических процессов в термодинамике особую группу составляют фазовые равновесия и превращения.
Термодинами́ческая фа́за[60] — макроскопическая физически однородная часть системы, отделённая от других частей системы поверхностями раздела. На границах скачком изменяются некоторые свойства системы.
Фазовым превращением называется процесс, в результате которого свойства тела меняются скачком.
Примеры:
1). Три фазы воды: лёд  жидкая вода
жидкая вода  пар.
пар.
2). Кристаллические модификации углерода: алмаз 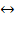 графит.
графит.
По числу фаз системы делятся на гомогенные и гетерогенные.
Гомогенная система – система, состоящая из одной фазы. Гетерогенная система – система, состоящая из двух или большего числа фаз.
При определенных условиях разные фазы одного и того же вещества могут находиться в равновесии друг с другом, соприкасаясь между собой. Равновесие двух фаз может иметь место лишь в определенном интервале температур, причем каждому значению температуры Т соответствует вполне определенное давление Р, при котором возможно равновесие. Таким образом, состояние равновесия двух фаз изобразится на диаграмме (Р, Т) линией.
В однокомпонентной системе разные фазы могут быть представлены различными агрегатными состояниями или разными полиморфными модификациями вещества. В многокомпонентной системе фазы могут иметь различный состав и структуру. В любом случае при наличии раздела фаз подразумевается принципиальная возможность перехода вещества из одной фазы в другую. Многофазная система находится в термодинамическом равновесии, если все её фазы находятся в механическом, тепловом и фазовом равновесии друг с другом.
Фазовые переходы I и II рода
Фазовые превращения бывают двух типов:
Фазовым переходом I рода называется фазовый переход, сопровождающийся скачкообразным изменением плотности, внутренней энергии, энтропии тела. Фазовые переходы I рода связаны с выделением или поглощением теплоты, называемой теплотой (скрытой теплотой) фазового перехода.
Пример:агрегатные превращения веществ (испарение, плавление, сублимация, переход твёрдого тела из одной кристаллической модификации в другую).
Фазовым переходом IIрода называется фазовый переход, при котором отсутствует скачкообразное изменение плотности, внутренней энергии и энтропии тела. Теплота фазового перехода II рода равна нулю. Фазовый переход II рода сопровождается скачкообразным изменением теплоёмкости и термодинамических коэффициентов расширяемости и сжимаемости.
Примеры:
1). Переход в точке Кюри ферромагнетика в парамагнетик (и наоборот).
2). Переход в сверхпроводящее состояние.
3). Переход жидкого гелия при Т = 2,2 К в сверхпроводящее состояние.
Ниже мы будем рассматривать фазовые переходы I рода.
Испарение и конденсация
Переход вещества в газообразное состояние называется парообразованием.
Совокупность молекул, вылетевших из вещества, называется паром этого вещества.
При парообразовании увеличиваются средние расстояния между молекулами. В результате потенциальная энергия взаимодействия частиц увеличивается (численное значение ее уменьшается, но она отрицательна). Таким образом, процесс парообразования связан с увеличением внутренней энергии вещества.
Парообразование может происходить непосредственно из твердого состояния — это возгонка (или сублимация). Все твёрдые тела в той или иной степени сублимируют.
Переход из жидкого состояния в газообразное возможен двумя различными процессами: испарением и кипением.
Испарение — это парообразование, происходящее только со свободной поверхности жидкости, граничащей с газообразной средой или с вакуумом, фазовый переход I рода.
Экспериментально установлены следующие закономерности:
1. При одинаковых условиях различные вещества испаряются с различной скоростью (скорость испарения определяется числом молекул, переходящих в пар с поверхности вещества за 1 с).
2. Скорость испарения тем больше:
· чем больше площадь свободной поверхности жидкости;
· чем меньше плотность паров над поверхностью жидкости. Скорость увеличивается при движении окружающего воздуха (ветер);
· чем больше температура жидкости.
При испарении температура тела понижается.
Механизм испарения можно объяснить с точки зрения молекулярно-кинетической теории: молекулы, находящиеся на поверхности, удерживаются силами притяжения со стороны других молекул вещества. Молекула может вылететь за пределы жидкости лишь тогда, когда ее кинетическая энергия превышает значение той работы, которую необходимо совершить, чтобы преодолеть силы молекулярного притяжения (работа выхода). Поэтому покинуть вещество могут только быстрые молекулы. В результате средняя кинетическая энергия оставшихся молекул уменьшается, а температура жидкости понижается.
Для поддержания температуры испаряющейся жидкости неизменной к ней необходимо подводить некоторое количество теплоты.
Количество теплоты Q, необходимое для превращения жидкости в пар при постоянной температуре, называется теплотой парообразования.
Экспериментально установлено, что Q = Lm, где m — масса испарившейся жидкости, L — удельная теплота парообразования.
Удельное тепло парообразованияL — величина, численно равная количеству теплоты, необходимому для превращения в пар жидкости единичной массы при неизменной температуре: L =  (
( 
Удельная теплота парообразования L зависит от рода жидкости и внешних условий. При увеличении температуры она уменьшается. Это объясняется тем, что все жидкости при нагревании расширяются. Расстояния между молекулами при этом увеличиваются и силы молекулярного взаимодействия уменьшаются. Кроме того, чем больше температура, тем больше средняя кинетическая энергия движения молекул и тем меньше энергии им нужно добавить, чтобы они могли вылететь за пределы поверхности жидкости.
Молекулы пара хаотически движутся. Поэтому скорости некоторых из них будут направлены в сторону жидкости. Достигнув поверхности, они втягиваются в нее силами притяжения со стороны молекул, находящихся на поверхности жидкости, и снова становятся молекулами жидкости.
Процесс перехода вещества из газообразного состояния в жидкое называется конденсацией.
Число возвратившихся в жидкость за определенный промежуток времени молекул тем больше, чем больше концентрация молекул пара, а, следовательно, чем больше давление пара над жидкостью. Конденсация пара сопровождается нагреванием жидкости. При конденсации выделяется такое же количество теплоты, которое было затрачено при испарении.
Испарение, сублимация и конденсация – примеры фазовых переходов I рода.
Равновесие жидкости и пара
Скорость испарения, т.е. количество жидкости, переходящей в пар за 1 с, зависит от внешнего давления и движения газообразной фазы над свободной поверхностью жидкости.
Рассмотрим процесс установления равновесия между жидкостью и её паром.
Пар, находящийся в динамическом равновесии со своей жидкостью, называется насыщенным (рис. 173).

Рис. 173.
Давление, при котором наблюдается равновесие между жидкостью и насыщенным паром, называется давлением (упругостью) насыщенного пара – Рн.п.
Давление насыщенного пара зависит от температуры. Каждой температуре соответствует определённое значение давления, при котором устанавливается подвижное равновесие (рис. 174; 175 ).
Пусть при любом промежуточном значении объёма V: mж, Vж – масса и объём вещества, находящегося в жидком состоянии; mп, Vп – масса и объём вещества, находящегося в парообразном состоянии; m = mп + mж – масса всего вещества.
Обозначим:  =
=  - удельный объём насыщенного пара;
- удельный объём насыщенного пара;  =
= 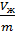 – удельный объём жидкости. Тогда: Vж =
– удельный объём жидкости. Тогда: Vж =  mж; Vп =
mж; Vп =  mп и V =
mп и V =  mж +
mж +  mп .
mп .
Последнее соотношение можно представить в виде: V = Vж  + Vп
+ Vп  .
.
Окончательно получим:  =
=  =
=  .
.
Таким образом, отношение масс жидкости и насыщенного пара в двухфазном состоянии равно отношению отрезков, на которые делит горизонтальный участок изотермы точка, изображающая состояние.

Рис. 174.
1 – 2  ненасыщенный пар; 2 – 3
ненасыщенный пар; 2 – 3  двухфазное состояние: насыщенный пар + жидкость; 3 – 4
двухфазное состояние: насыщенный пар + жидкость; 3 – 4  жидкость; V3 – объём сконденсированной жидкости;
жидкость; V3 – объём сконденсированной жидкости;
V2 – объём ненасыщенного пара.

Рис. 175.
Этот результат можно обобщить на все двухфазные состояния, изображённые изотермой в координатах (P,V).
Пусть V1 и V2 – концы горизонтального участка изотермы, занимаемого веществом в первой и второй фазах. Тогда: 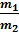 =
=  , где m1 и m2 – массы вещества в первой и второй фазах.
, где m1 и m2 – массы вещества в первой и второй фазах.
Метастабильные состояния
Метастабильное состояние (от греч. μετα «через» и лат. stabilis «устойчивый») — состояние квазиустойчивого равновесия физической системы, в котором система может находиться длительное время.
Что такое метастабильное состояние, может быть понятно из рис. 176:
· состояние 1: метастабильное — состояние, стабильность которого сохраняется при не очень больших возмущениях;
· состояние 2: нестабильное — состояние, стабильность которого нарушается при сколь угодно малых возмущениях;
· состояние 3: стабильное — состояние, стабильность которого сохраняется при больших возмущениях.
Метастабильные состояния широко встречаются в природе и используются в науке и технике. С существованием метастабильных состояний связаны, например, явления магнитного, электрического и упругого гистерезиса, образование перенасыщенных растворов, закалка стали, производство стекла и т. д.
Поглощение энергии при испарении жидкости и выделение ее

Рис. 176.
Большой класс метастабильных состояний связан с фазовыми переходами 1-го рода (кристалл  жидкость жидкость  газ).
В термодинамике метастаби́льное состоя́ние - состояние неустойчивого равновесия физической макроскопической системы, в котором система может находиться длительное время.
Возникновение метастабильных состояний объясняется теорией термодинамического равновесия. Состоянию равновесия замкнутой системы соответствует максимум энтропии S. При постоянном объёме V и температуре Т равновесию отвечает минимум свободной энергии F (гельмгольцевой энергии), а при постоянном давлении P и температуре Т — минимум термодинамического потенциала G (гиббсовой энергии). Однако определённым значениям внешних параметров (P, V, Т и др.) может соответствовать несколько экстремумов (максимумов или минимумов) одной из перечисленных выше функций. Каждому из относительных минимумов функции F или G соответствует устойчивое по отношению к малым воздействиям или флуктуациям состояние. Такие состояния называют метастабильными. При небольшом отклонении от метастабильного состояния система возвращается в это же состояние, однако по отношению к большим отклонениям от равновесия она неустойчива и переходит в состояние с абсолютным минимумом термодинамического потенциала, которое устойчиво по отношению к конечным отклонениям значений физических параметров от равновесных. Таким образом, хотя метастабильное состояние в известных пределах устойчиво, рано или поздно система всё же переходит в абсолютно устойчивое, стабильное состояние.
В квантовых системах метастабильные состояния — состояния с временем жизни ( газ).
В термодинамике метастаби́льное состоя́ние - состояние неустойчивого равновесия физической макроскопической системы, в котором система может находиться длительное время.
Возникновение метастабильных состояний объясняется теорией термодинамического равновесия. Состоянию равновесия замкнутой системы соответствует максимум энтропии S. При постоянном объёме V и температуре Т равновесию отвечает минимум свободной энергии F (гельмгольцевой энергии), а при постоянном давлении P и температуре Т — минимум термодинамического потенциала G (гиббсовой энергии). Однако определённым значениям внешних параметров (P, V, Т и др.) может соответствовать несколько экстремумов (максимумов или минимумов) одной из перечисленных выше функций. Каждому из относительных минимумов функции F или G соответствует устойчивое по отношению к малым воздействиям или флуктуациям состояние. Такие состояния называют метастабильными. При небольшом отклонении от метастабильного состояния система возвращается в это же состояние, однако по отношению к большим отклонениям от равновесия она неустойчива и переходит в состояние с абсолютным минимумом термодинамического потенциала, которое устойчиво по отношению к конечным отклонениям значений физических параметров от равновесных. Таким образом, хотя метастабильное состояние в известных пределах устойчиво, рано или поздно система всё же переходит в абсолютно устойчивое, стабильное состояние.
В квантовых системах метастабильные состояния — состояния с временем жизни (  ), много большим характерного времени жизни возбуждённых состояний (10-8 с) атомной системы. Обычно метастабильными считают возбуждённые состояния, излучательные (радиационные), переходы из которых в другие состояния запрещены строгими правилами отбора. Метастабильные состояния отличаются типом переходов, которые для них возможны: магнитный дипольный, электрический квадрупольный, двухфотонный и другие переходы.
Пересыщенный пар. Перегретая жидкость
Примерами метастабильных состояний могут служить перегретая или переохлажденная жидкость и переохлажденный (пересыщенный) пар.
Из сопоставления изотермы Ван-дер-Ваальса с реальной изотермой вытекает, что эти изотермы примерно совпадают на участках, отвечающих однофазным состояниям вещества, но ведут себя различно в области расслоения на две фазы. Вместо S-образного завитка на изотерме Ван-дер-Ваальса реальная изотерма имеет в этой области прямолинейный горизонтальный участок F – G (рис. 177). ), много большим характерного времени жизни возбуждённых состояний (10-8 с) атомной системы. Обычно метастабильными считают возбуждённые состояния, излучательные (радиационные), переходы из которых в другие состояния запрещены строгими правилами отбора. Метастабильные состояния отличаются типом переходов, которые для них возможны: магнитный дипольный, электрический квадрупольный, двухфотонный и другие переходы.
Пересыщенный пар. Перегретая жидкость
Примерами метастабильных состояний могут служить перегретая или переохлажденная жидкость и переохлажденный (пересыщенный) пар.
Из сопоставления изотермы Ван-дер-Ваальса с реальной изотермой вытекает, что эти изотермы примерно совпадают на участках, отвечающих однофазным состояниям вещества, но ведут себя различно в области расслоения на две фазы. Вместо S-образного завитка на изотерме Ван-дер-Ваальса реальная изотерма имеет в этой области прямолинейный горизонтальный участок F – G (рис. 177).
 Рис. 177. Изотермы реального газа (пара).
Синие кривые — изотермы при температуре ниже критической, зелёные участки на них — метастабильные состояния. Участок правее точки G — обычный пар. Участок GC — пересыщенный пар. Прямая GF — обычный переход пар↔жидкость, динамическое равновесие между жидкостью и насыщенным паром. Участок FA — перегретая жидкость. Участок левее точки F — нормальная жидкость.
В области перехода жидкость
Рис. 177. Изотермы реального газа (пара).
Синие кривые — изотермы при температуре ниже критической, зелёные участки на них — метастабильные состояния. Участок правее точки G — обычный пар. Участок GC — пересыщенный пар. Прямая GF — обычный переход пар↔жидкость, динамическое равновесие между жидкостью и насыщенным паром. Участок FA — перегретая жидкость. Участок левее точки F — нормальная жидкость.
В области перехода жидкость  пар реальная изотерма отклоняется от ванн – дер – ваальсовской кривой (рис. 177). Однако участки кривой F – A и C- G Ван – дер - Ваальса описывают метастабильные состояния: F – A – перегретая жидкость (отсутствуют зародыши газовой фазы: пузырьки газа и т.д.); C- G – переохлаждённый (пересышенный) пар (процесс конденсации начаться не может, т.к. отсутствуют центры конденсации).
Пересы́щенный пар — пар, давление которого превышает давление насыщенного пара при данной температуре. Может быть получен путём увеличения давления пара в объёме, свободном от центров конденсации (пылинок, ионов, капелек жидкости малых размеров и т. д.). Другой способ получения — охлаждение насыщенного пара при тех же условиях. В связи с последним способом получения насыщенного пара применительно к нему используется также наименование переохлаждённый пар. Кроме того, иногда в литературе встречается термин перенасыщенный пар.
Состояние пересыщенного пара является метастабильным, то есть такое состояние пара способно существовать длительное время, однако оно является термодинамически неустойчивым. Так, при появлении каких-либо центров конденсации часть пара конденсируется, давление оставшегося пара падает, и он переходит в устойчивое состояние насыщенного пара над сконденсировавшейся жидкостью. Устанавливается динамическое равновесие между жидкой и газообразной фазами.
В природе пересыщенный водяной пар образуется, например, при подъёме нагретых у поверхности земли воздушных масс и последующем их охлаждении, вызванном адиабатическим расширением.
Перегре́тая жи́дкость — жидкость, нагретая выше температуры кипения.
Жидкость, например, воду, тщательно очищенную от посторонних твёрдых частичек и пузырьков газа (центров парообразования), можно нагреть до температуры, превышающей температуру кипения при данном давлении. Если в перегретой жидкости возникнут центры парообразования (или их введут искусственно), то жидкость взрывообразно перейдёт в пар — устойчивое при данной температуре состояние.
Таким образом, пересыщенным паром и перегретой жидкостью могут быть только очень чистые, не содержащие примесей, пар и жидкость. Переохлаждённый пар является рабочим веществом в камере Вильсона, а перегретая жидкость – в пузырьковой камере, используемых для регистрации заряженных частиц.
Критическое состояние
Рассмотрим изотермы реального газа для нескольких значений температуры (рис. 178). С повышением температуры горизонтальный участок изотермы сокращается, стягиваясь в точку при Т = Ткр. – точку К,точка перегиба, называемая критической точкой, а температура Ткр. – критической температурой. пар реальная изотерма отклоняется от ванн – дер – ваальсовской кривой (рис. 177). Однако участки кривой F – A и C- G Ван – дер - Ваальса описывают метастабильные состояния: F – A – перегретая жидкость (отсутствуют зародыши газовой фазы: пузырьки газа и т.д.); C- G – переохлаждённый (пересышенный) пар (процесс конденсации начаться не может, т.к. отсутствуют центры конденсации).
Пересы́щенный пар — пар, давление которого превышает давление насыщенного пара при данной температуре. Может быть получен путём увеличения давления пара в объёме, свободном от центров конденсации (пылинок, ионов, капелек жидкости малых размеров и т. д.). Другой способ получения — охлаждение насыщенного пара при тех же условиях. В связи с последним способом получения насыщенного пара применительно к нему используется также наименование переохлаждённый пар. Кроме того, иногда в литературе встречается термин перенасыщенный пар.
Состояние пересыщенного пара является метастабильным, то есть такое состояние пара способно существовать длительное время, однако оно является термодинамически неустойчивым. Так, при появлении каких-либо центров конденсации часть пара конденсируется, давление оставшегося пара падает, и он переходит в устойчивое состояние насыщенного пара над сконденсировавшейся жидкостью. Устанавливается динамическое равновесие между жидкой и газообразной фазами.
В природе пересыщенный водяной пар образуется, например, при подъёме нагретых у поверхности земли воздушных масс и последующем их охлаждении, вызванном адиабатическим расширением.
Перегре́тая жи́дкость — жидкость, нагретая выше температуры кипения.
Жидкость, например, воду, тщательно очищенную от посторонних твёрдых частичек и пузырьков газа (центров парообразования), можно нагреть до температуры, превышающей температуру кипения при данном давлении. Если в перегретой жидкости возникнут центры парообразования (или их введут искусственно), то жидкость взрывообразно перейдёт в пар — устойчивое при данной температуре состояние.
Таким образом, пересыщенным паром и перегретой жидкостью могут быть только очень чистые, не содержащие примесей, пар и жидкость. Переохлаждённый пар является рабочим веществом в камере Вильсона, а перегретая жидкость – в пузырьковой камере, используемых для регистрации заряженных частиц.
Критическое состояние
Рассмотрим изотермы реального газа для нескольких значений температуры (рис. 178). С повышением температуры горизонтальный участок изотермы сокращается, стягиваясь в точку при Т = Ткр. – точку К,точка перегиба, называемая критической точкой, а температура Ткр. – критической температурой.
 Рис. 178.
Касательная к изотерме в точке К расположена параллельно оси V. Состояние, изображаемое точкой К называется критическим состоянием вещества.
Понятие критической температуры было введено в 1860 г. Д.И.Менделеевым.
Критическое состояние - 1) предельное состояние равновесия двухфазных систем, в котором обе сосуществующие фазы становятся тождественными по своим свойствам; 2) состояние вещества в точках фазовых переходов II рода.
Критическое состояние, являющееся предельным случаем равновесия двухфазных систем, наблюдается в чистых веществах при равновесии жидкость — газ, а в растворах — при фазовых равновесиях газ — газ, жидкость — жидкость, жидкость — газ, твёрдое тело — твёрдое тело. За пределами критического состояния сосуществование рассматриваемых фаз в равновесии невозможно, система превращается в однофазную (гомогенную) систему.
Рис. 178.
Касательная к изотерме в точке К расположена параллельно оси V. Состояние, изображаемое точкой К называется критическим состоянием вещества.
Понятие критической температуры было введено в 1860 г. Д.И.Менделеевым.
Критическое состояние - 1) предельное состояние равновесия двухфазных систем, в котором обе сосуществующие фазы становятся тождественными по своим свойствам; 2) состояние вещества в точках фазовых переходов II рода.
Критическое состояние, являющееся предельным случаем равновесия двухфазных систем, наблюдается в чистых веществах при равновесии жидкость — газ, а в растворах — при фазовых равновесиях газ — газ, жидкость — жидкость, жидкость — газ, твёрдое тело — твёрдое тело. За пределами критического состояния сосуществование рассматриваемых фаз в равновесии невозможно, система превращается в однофазную (гомогенную) систему.
В критическом состоянии уменьшается различие в удельных объемах, а следовательно, и в плотностях жидкости и насыщенного пара. При критической температуре это различие полностью исчезает. Одновременно исчезает всякое различие между жидкостью и паром. Температурный ход плотности жидкости и насыщенного пара показан на рис. 179.
Рис. 179. Объем Vкр., давление Ркр., и температура Ткр., отвечающие критическому состоянию, называются критическими параметрами. Из рис. 178 следует, что давление насыщенного пара растет с температурой, достигая при критической температуре значения. При температурах выше критической (Т >Ткр. ) понятие насыщенного пара теряет смысл. Поэтому кривая зависимости давления насыщенного пара от температуры заканчивается в критической точке. Если провести линию через крайние точки горизонтальных участков изотерм (рис. 180), получается колоколообразная кривая, ограничивающая область двухфазных состояний вещества. При температурах выше критической вещество при любом давлении оказывается однородным. Колоколообразная кривая и участок критической изотермы, лежащий слева от точки делят диаграмму (V) на три области (рис. 180). Наклонной штриховкой помечена область однородных жидких состояний вещества. Под колоколообразной кривой располагается область двухфазных состояний и, наконец, область, лежащая справа от колоколообразной кривой и верхней ветви критической изотермы, представляет собой область однородных газообразных состояний вещества. В последней можно особо выделить часть, лежащую под правой ветвью критической изотермы, назвав ее областью пара. | |||

Рис. 180.
Любое состояние в этой области отличается от остальных газообразных состояний в том отношении, что при изотермическом сжатии вещество, первоначально находившееся в таком состоянии, претерпевает процесс сжижения. Вещество, находящееся в одном из состояний при температуре выше критической, не может быть сжижено никаким сжатием. Подразделение газообразных состояний на газ и пар не является общепринятым.
Выбрав процесс перехода так, чтобы он не пересекал двухфазную область, можно осуществить переход из жидкого состояния в газообразное (и обратно) без расслаивания вещества на две фазы. В этом случае в процессе перехода вещество будет всё время оставаться однородным (рис. 181).

Рис. 181.
Плавление и кристаллизация
Плавлением называют процесс перехода вещества из твердого кристаллического состояния в жидкое.
Переход кристаллического тела в жидкое состояние происходит при определенной для каждого вещества температуре Тпл. – температуре плавления и требует затраты некоторого количества тепла Qпл., называемого теплотой плавления[61].
Таким образом, переход из кристаллического в жидкое состояние происходит при вполне определенных условиях, характеризуемых значениями давления и температуры. Совокупности этих значений соответствует кривая на диаграмме (Т-  ), которую принято называть кривой плавления (рис. 182). Точки кривой плавления определяют условия, при которых кристаллическая и жидкая фазы могут находиться в равновесии друг с другом.
), которую принято называть кривой плавления (рис. 182). Точки кривой плавления определяют условия, при которых кристаллическая и жидкая фазы могут находиться в равновесии друг с другом.

Рис. 182.
Если веществу, первоначально находившемуся в кристаллическом состоянии, сообщать каждую секунду одно и то же количество тепла, то изменение температуры тела со временем будет таким, как показано на рис. 182 и 183. В начале температура тела все время растет. По достижении температуры плавления (точка 1 на рис. 183), несмотря на то, что к телу по-прежнему продолжает подводиться тепло, температура его перестает изменяться. Одновременно начинается процесс плавления твердого тела, в ходе которого все новые и новые порции вещества превращаются в жидкость. После того как процесс плавления будет закончен и все вещество полностью перейдет в жидкое состояние (точка 2 на рис. 183), температура снова начнет повышаться.

Рис. 183.
Количество теплоты Qпл., которое необходимо подвести единице массы твёрдого тела при постоянной температуре Тпл. для осуществления процесса плавления, называется удельной теплотой плавления:  =
= 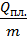 , (
, (  ). Каждому кристаллу присуща своя величина удельной теплоты плавления.
). Каждому кристаллу присуща своя величина удельной теплоты плавления.
Плавление происходит при постоянной температуре с поглощением тепла. Постоянство температуры объясняется тем, что при плавлении вся подводимая теплота идет на разупорядочение регулярного пространственного расположения атомов (молекул) в кристаллической решетке. При этом среднее расстояние между атомами и, следовательно, силы взаимодействия изменяется незначительно.
Температура плавления для данного кристалла Тпл. его важная характеристика, но она не является величиной постоянной, а существенным образом зависит от внешнего давления, при котором происходит плавление. Для большинства кристаллов (кроме воды, и некоторых сплавов) температура плавления растет с увеличением внешнего давления, так как для отдаления атомов друг от друга при большем давлении требуется большая энергия тепловых движений, т. е. более высокая температура.
В случае аморфного тела его температура по мере подвода тепла непрерывно растёт. Для аморфных тел нет определённой температуры перехода в жидкое состояние. Этот переход совершается непрерывно, а не скачком. У аморфных тел изменение температуры со временем (пунктирная кривая на рис. 183) не имеет участка с постоянной температурой, а только точку перегиба. У аморфных тел нельзя указать такую определенную температуру, выше которой можно было бы констатировать жидкое состояние, а ниже - твердое состояние. Выделяется только температура, соответствующая точке перегиба. Эту температуру условно называют температурой размягчения аморфных тел. Это объясняется тем, что жидкости и аморфные тела отличаются лишь степенью подвижности молекул, — аморфные тела, как уже отмечалось, представляют собой сильно переохлажденные жидкости. Увеличение температуры твердого аморфного тела сопровождается непрерывным уменьшением его вязкости.
Процесс плавления – фазовый переход I рода, связан с возрастанием энтропии системы, как переход из более упорядоченного состояния в менее упорядоченное, жидкое.
При охлаждении жидкостей до некоторой температуры жидкой фазы Ткрист. – температуры кристаллизации, начинается переход вещества из жидкого в твёрдое кристаллическое состояние (кристаллизация). Кристаллизация связана с выделением количества теплоты, равного теплоте плавления, и для химически чистых жидкостей протекает при постоянной температуре, причём Тпл. = Ткрист. (рис. 184).

Рис. 184.
В кристалле каждая молекула совершает только колебательное движение, тогда как в жидкости она совершает еще и поступательное движение. Поэтому при кристаллизации от вещества необходимо отводить тепловую энергию, соответствующую поступательному движению молекул. Молекулы, утратившие этот излишек энергии, присоединяются к кристаллам.
В процессе кристаллизации упорядочивается движение частиц жидкости, увеличивается время их «оседлого» существования – время релаксации. Постепенно движения частиц превращаются в связанные тепловые колебания около узлов кристаллической решётки.
Процесс кристаллизациипротекает следующим образом.
Для начала кристаллизации необходимо, чтобы в жидкости имелись центры кристаллизации – зародыши кристаллической фазы (примеси, пылинки, пузырьки газа). В этих местах в первую очередь возникает правильное взаимное расположение частиц. При охлаждении жидкости до температуры, при которой твердая и жидкая фазы могут находиться в равновесии при данном давлении начинается одновременный рост кристалликов вокруг центров кристаллизации. Разрастаясь все более, отдельные кристаллики в конце концов смыкаются друг с другом, образуя поликристаллическое твердое тело.
Если в жидкости отсутствуют центры кристаллизации и от неё достаточно медленно и равномерно отводится теплота, то жидкость может быть охлаждена до более низкой температуры, чем Ткрист. (переохлаждённая жидкость). Это состояние жидкости является метастабильным. Обычно достаточно попасть в такую жидкость пылинке, для того чтобы она распалась на жидкость и кристаллы, находящиеся при равновесной температуре. Однако в некоторых случаях при больших переохлаждениях подвижность молекул жидкости оказываемся столь незначительной, что метастабильное состояние может сохраняться очень долго. Жидкость в таких случаях обладает весьма малой текучестью и представляет собой аморфное твердое тело.
Уравнение Клапейрона – Клаузиуса
Характерной особенностью всех фазовых переходов I состоит в том, что в этих процессах постоянные величины давление и температура, но зато изменяются соотношение между массами двух фаз. Второй особенностью этих процессов является то, что для их осуществления необходимо подводить к системе или отводить от неё некоторое количество теплоты Q, называемой теплотой фазового перехода.
Cвязь удельной теплоты фазового перехода r с температурой Т и давлением Р фазового перехода устанавливает уравнение Клапейрона – Клаузиуса.
Уравнение Клапейрона — Клаузиуса — термодинамическое уравнение, относящееся к квазистатическим (равновесным) процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация, полиморфное превращение и др.).
Согласно этому уравнению, теплота фазового перехода (например, теплота испарения, теплота плавления) при квазистатическом процессе определяется выражением:
 =
= 
где r =  — удельная теплота фазового перехода, ∆
— удельная теплота фазового перехода, ∆  — изменение удельного объёма тела при фазовом переходе.
— изменение удельного объёма тела при фазовом переходе.
Уравнение Клапейрона – Клаузиуса можно представить в виде: r =(  -
- 
 .Часто уравнение Клапейрона — Клаузиуса записывают относительно производных
.Часто уравнение Клапейрона — Клаузиуса записывают относительно производных  или
или  :
:  =
=  .
.
Для процессов испарения и сублимации  выражает изменение давления насыщенного пара P с температурой Т, а для процессов плавления и полиморфного превращения
выражает изменение давления насыщенного пара P с температурой Т, а для процессов плавления и полиморфного превращения  определяет изменение температуры перехода с давлением. Иными словами, уравнение Клапейрона — Клаузиуса является дифференциальным уравнением кривой фазового равновесия в переменных P, Т.
определяет изменение температуры перехода с давлением. Иными словами, уравнение Клапейрона — Клаузиуса является дифференциальным уравнением кривой фазового равновесия в переменных P, Т.
Уравнение Клапейрона – Клаузиуса широко используется в теплотехнике, т.к. оно может служить для расчёта любой из величин, входящих в уравнение, если остальные известны. В частности, с его помощью рассчитывают теплоты испарения, экспериментальное определение которых сопряжено со значительными трудностями.
Для решения уравнения Клапейрона — Клаузиуса необходимо знать, как изменяются с температурой и давлением величины удельной теплоты фазового перехода r и объёмов фаз V1 и V2, что представляет сложную задачу. Обычно эту зависимость устанавливают эмпирически и решают уравнение Клапейрона — Клаузиуса численно.
Уравнение Клапейрона — Клаузиуса применимо как к чистым веществам, так и к растворам и отдельным компонентам растворов. В последнем случае уравнения Клапейрона — Клаузиуса связывает парциальное давление насыщенного пара данного компонента с его парциальной теплотой испарения.
Согласно уравнению Клапейрона - Клаузиуса знак производной зависит от того, каким изменением объема — возрастанием или уменьшением — сопровождается фазовый переход, происходящий при поглощении тепла. При испарении жидкости или твердого тела объем всегда возрастает, поэтому для кривой испарения, а также для кривой сублимации может быть только положительной: повышение температуры приводит к увеличению равновесного давления. При плавлении объем, как правило, возрастает, так что увеличение давления приводит к повышению температуры плавления. Однако у некоторых веществ, к числу которых принадлежит и вода, объем жидкой фазы меньше объема твердой фазы. В этом случае — увеличение давления сопровождается понижением температуры плавления. Подвергнув лед сильному сжатию, можно, не повышая температуры выше 0°С, вызвать его плавление. Температура перехода из одной кристаллической модификации в другую будет повышаться или понижаться с ростом давления в зависимости от того, какая из твердых фаз обладает большим удельным объемом.
Таким образом, знак производной  зависит от того, каким изменением объёма – возрастанием или уменьшением – сопровождает фазовый переход I рода:
зависит от того, каким изменением объёма – возрастанием или уменьшением – сопровождает фазовый переход I рода:  > 0 – объём возрастает;
> 0 – объём возрастает;  < 0 - объём убывает.
< 0 - объём убывает.
Уравнение Клапейрона — Клаузиуса применимо к любым фазовым переходам, сопровождающимся поглощением или выделением теплоты (фазовым переходом I рода), и является прямым следствием условий фазового равновесия, из которых оно и выводится.
Элементарный вывод уравнения Клапейрона – Клаузиуса
Пусть некоторое количество вещества совершает очень узкий цикл Карно (рис. 185). Для вывода существенен горизонтальный участок изотермы, соответствующий фазовому переходу. Слева и справа от этого участка всё вещество находится в одной фазе. Осуществим цикл Карно при бесконечно малой разности температур следующим образом: сначала сообщаем телу теплоту, переводя его изотермически из состояния 1 в состояние 2, затем адиабатически охлаждаем его на температуру dT, после чего замыкаем цикл, отводя теплоту и переводя вещество в фазу 1 с последующим адиабатическим нагревом. Совершённая работа равна площади цикла: 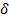 A = dP (V2 – V1), где V2 – V1) — изменение объёма вещества при переходе его из первой фазы во вторую.
A = dP (V2 – V1), где V2 – V1) — изменение объёма вещества при переходе его из первой фазы во вторую.

Рис. 185.
С другой стороны: 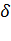 A =
A =  r, где КПД цикла Карно
r, где КПД цикла Карно  =
=  ; dT – разность температур между изотермами цикла Карно (рис. 185).
; dT – разность температур между изотермами цикла Карно (рис. 185).
Тогда получаем: ( 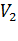 -
-  dP = r
dP = r  или
или  =
=  – уравнение Клапейрона – Клаузиуса.
– уравнение Клапейрона – Клаузиуса.
Диаграмма состояния. Тройная точка
Как уже указывалось, одно и то же вещество может находиться в одном из трех агрегатных состояний в зависимости от внешних условий температуры и давления.
Зависимость агрегатного состояния вещества от давления и температуры может быть наглядно представлена диаграммой состояния.
Для каждого вещества на основе экспериментальных данных можно составить диаграмму состояний в координатах Р и Т, по которой легко определить, в каком состоянии будет находиться это вещество и что с ним будет происходить при изменении внешних условий. Для ее построения, откладывая по оси ординат давление Р, а по оси абсцисс температуру Т, отмечают точками такие сочетания давления Р и температуры Т, при которых находятся в динамическом равновесии жидкость — газ, газ — твердое тело, жидкость — твердое тело. Каждая точка на диаграмме соответствует равновесному состоянию вещества, т. е. такому, в котором оно может находиться неопределенно долгое время.
Из правила фаз Гиббса[62] следует, что химически однородное вещество (однокомпонентная система) в равновесии не может иметь больше трёх фаз.
Если для одного и того же вещества построить на диаграмме Т – Р кривые равновесия жидкость – пар и твёрдое тело – жидкость, то они пересекутся в некоторой точке Тр., характеризующейся некоторыми определёнными значениями температуры Ттр. и давления Ртр. (рис. 186). Точка Тр. – тройная точка.

Рис. 186.
Тройная точка - точка пересечения кривых фазового равновесия на плоской диаграмме состояния вещества, соответствующая устойчивому равновесию трёх фаз.
В этой точке сходятся линии плавления, кипения и возгонки (сублимации). Температура Ттр., соответствующее ей давление Ртр. – единственные значения температуры и давления, при которых могут находиться в равновесии три фазы вещества: твёрдая, жидкая и газообразная.
Часть диаграммы слева от линии соответствует твердому состоянию вещества; область, ограниченная линией — жидкому, а область справа от линии — газообразному состоянию. Линия соответствует равновесию жидкой и газообразной фаз, линия — равновесию жидкой и твердой фаз и — равновесию твердой и газообразной фаз.
В однокомпонентном веществе только кривая испарения имеет конец – критическую точку К. Кривая плавления – кристаллизации, сублимации уходят в бесконечность, либо заканчиваются на тройных точках. Отсутствие конца типа критической точки у кривой плавления говорит о том, что жидкая и твёрдая фазы принципиально отличаются друг от друга. Главное в этом отличии заключается в том, что жидкости изотропны, а кристаллы – анизотропны.
При давлениях Р < Ртр. вещество не может существовать в жидкой фазе ни при каких температурах.
Пример.
| Вещество | tтр. oC | Pтр., Па |
| Вода | 0,01 | |
| Углекислота | - 56,7 | 5,17•105 |
При давлениях, близких к атмосферному, углекислота может существовать только в твёрдом («сухой лёд») и газообразном состояниях (сублимирует). У большинства твёрдых тел давление насыщенных паров так мало, что испарение не играет существенной роли. У них тройная точка лежит значительно ниже атмосферного давления, поэтому переход из твёрдого состояния в газообразное осуществляется через промежуточную жидкую фазу.
Тройная точка существует у всех веществ, кроме гелия. Поведение гелия при низких температурах квантовым эффектом.
[1] Система ортов (или базисная система векторов) - это система единичных векторов осей координат. Орт координатной оси  обозначается через
обозначается через 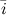 , оси
, оси 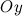 - через
- через  , оси
, оси  - через
- через 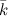 (рис. 3).
(рис. 3).

Рис.3.
Если вектор  (ax; ay; az) расположен в пространстве, то разложение по ортам координатных осей имеет вид:
(ax; ay; az) расположен в пространстве, то разложение по ортам координатных осей имеет вид:  ax
ax  +ay
+ay  + az
+ az  . .
. .
[2] Метр (русское обозначение: м; международное: m; от др.-греч. μέτρον — мера, измеритель) — единица измерения длины и расстояния в Международной системе единиц (СИ), одна из семи основных единиц СИ. Метр равен расстоянию, которое проходит свет в вакууме за промежуток времени, равный  секунды.
секунды.
[3] Секу́нда (русское обозначение: с; международное: s) — единица измерения времени, одна из основных единиц Международной системы единиц (СИ) ; представляет собой интервал времени, равный 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного (квантового) состояния атома цезия-133 в покое при 0 К при отсутствии возмущения внешними полями.
[4] Релятивистские эффекты ( лат. relativus – относительный) – эффекты, проявляющиеся при движении тел со скоростью близкой к скорости света в вакууме ( 
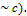
[5] Угловая скорость  - аксиальный вектор. Аксиальные векторы не связаны с определенной линией действия. Их можно перемещать в пространстве параллельно самим себе (свободные векторы).
- аксиальный вектор. Аксиальные векторы не связаны с определенной линией действия. Их можно перемещать в пространстве параллельно самим себе (свободные векторы).
[6] Килограмм есть единица массы, равная массе международного прототипа килограмма (прототип (эталон) килограмма, хранится в Международном бюро мер и весов (расположено в Севре близ Парижа) и представляет собой цилиндр диаметром и высотой 39,17 мм из платино-иридиевого сплава (90 % платины, 10 % иридия)).
[7] Ньютон (русское обозначение: Н; международное: N) — единица измерения силы в Международной системе единиц (СИ). Ньютон — производная единица. Исходя из второго закона Ньютона она определяется как сила, изменяющая за 1 с скорость тела массой 1 кг на 1 м/с в направлении действия силы. Таким образом, 1 Н = 1 кг·м/с2.
[8] Диссипа́ция (лат. dissipatio) — рассеивание. Диссипация энергии — переход части энергии упорядоченных процессов (кинетической энергии движущегося тела, энергии электрического тока и т. д.) в энергию неупорядоченных процессов, в конечном итоге — в тепло.
[9] Ньютон И. (1643-1727) – выдающийся английский учёный, основоположник механической картины мира.
[10] Однор́одность пространства означает, что нет такой точки в пространстве, относительно которой существует некоторая «выделенная» симметрия, все точки равноправны, поэтому рассматриваемый эксперимент не зависит от нашего выбора точки отсчета, т.е. пространство называется однородным, если параллельный перенос системы отсчета не влияет на результат измерений. Однородность пространства и времени означает, что наблюдаемые физические свойства и явления должны быть одинаковы в любой точке пространства и в любой момент времени.
[11] Абсолютное пространство — в классической механике — трёхмерное евклидово пространство, в котором выполняется принцип относительности и преобразования Галилея. Термин введён Ньютоном (вместе с концепцией абсолютного времени). Пространство и время у него выступают в качестве универсального вместилища, обладающего отношениями порядка и существующие независимо как друг от друга, так и материальных тел.
[12] В общем случае сила 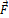 , действующая на материальную частицу, изменяется вместе с изменением координат частицы, т.е. F = f(x, y,z), поэтому элементарная работа не является полным дифференциалом и её нельзя обозначать dA.
, действующая на материальную частицу, изменяется вместе с изменением координат частицы, т.е. F = f(x, y,z), поэтому элементарная работа не является полным дифференциалом и её нельзя обозначать dA.
[13] Джоуль - это работа, совершаемая силой 1 Н на перемещении 1 м, если направления силы и перемещения совпадают: [ Дж = Н•м].
[14] Potentia (лат.) – сила.
[15] Гамильтон У.Р. (1805-1865) – ирландский математик.
[16] Однородность времени – это тожественность всех временных точек (моментов времени) на временной оси; означает, что любые явления, которые происходят в одних и тех же условиях, но в разные периоды времени, протекают одинаково. Согласно теореме Э.Нетер следствием однородности времени является закон сохранения энергии.
[17] Изотропи́я, изотро́пность (из др.-греч. ί̓σος «равный, одинаковый, подобный» + τρόπος «оборот, поворот; характер») — одинаковость физических свойств во всех направлениях, инвариантность, симметрия по отношению к выбору направления. Пространство называется изотропным, если поворот системы отсчета на произвольный угол не приведет к изменению результатов измерений.
[18] Паскаль Б. (1623 – 1662) – французский учёный.
[19] Архимед (3 в. до н.э.) – древнегреческий учёный.
[20] Градие́нт (от лат. gradiens, род. падеж gradientis — шагающий, растущий) — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины  , значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный быстроте роста этой величины в этом направлении.
, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный быстроте роста этой величины в этом направлении.
[21] Капица С.П. (1894 – 1984) – советский физик, лауреат Нобелевской премии.
[22] Рейнольдс О. (1842-1912) – английский физик.
[23] Бернулли Д. (1700-1782) – швейцарский физик, член Петербургской Академии наук.
[24] Дальтон Д. (1766-1844) – английский физик и химик, создатель химического атомизма.
[25] Авогадро А. (1776-1856) – итальянский физик и химик. В 1811 г. выдвинул молекулярную гипотезу строения вещества, установил один из газовых законов, названных его именем.
[26] Больцман Л. (1844-1906) – австрийский физик, один из основателей статистической физики.
[27] Максвелл Д.К. (1831-1879) – английский физик, создатель классической электродинамики, один из основоположников статистической физики, организатор Кавендишской лаборатории.
[28] Клаузиус Р.Ю. (1882-1888) – немецкий физик один из основателей термодинамики и молекулярно-кинетической теории, иностранный член Петербургской АН.
[29] Менделеев Д.И. (1834-1907) – выдающийся русский химик и физик.
[30] Клапейрон Б.П.Э. (1799-1864) – французский физик и инженер, член-корр. Петербургской АН.
[31] Бойль Р. (1627-1691) – английский физик и химик, один из учредителей Лондонского королевского общества.
[32] Мариотт Э. (1620-1684) - французский физик.
[33] Гей-Люссак Ж.Л. (1778-1850) – французский физик и химик.
[34] Шарль Ж. – французский учёный.
[35] Дальтон Д. (1766-18440 – английский химик и физик, создатель химического атомизма..
[36] Майер Ю.Р. (1814-1878) – английский естествоиспытатель, врач.
[37] Гельмгольц Г.Л. Ф. (1821-1894) – немецкий учёный, иностранный член Петербургской АН.
[38] Вечный двигатель первого рода – периодически действующий двигатель, который совершал бы большую работу, чем сообщённая ему извне энергия.
[39] Вырожденный газ - это такой, к которому неприменима классическая статистика (обычная газовая термодинамика).
[40] Карно С. (1796 – 1832) – французский физик и инженер, один из создателей термодинамики.
[41] Оствальд В.Ф. (1853 – 1932) – немецкий физико-химик и философ-идеалист; иностранный член-корреспондент Петербургской АН.
[42] Полный дифференциал функции двух независимых переменных равен сумме произведений частных производных функции на дифференциалы соответствующих независимых переменных:

[43] Нернст В. (1864-1941) – немецкий физико - химик, иностранный почётный член АН СССР.
[44] Гельмгольц Г.Л.Ф. (1821-1894) – немецкий учёный, иностранный член Петербургской АН.
[45] Гиббс Д.У. (1839-1903) – американский физик – теоретик, один из основателей термодинамики и статистической механики.
[46] Вероятностью события называется отношение числа случаев, благоприятных для данного события, к общему числу всех равновозможных случаев.
[47] Ландау Л.Д. (1908-1968) – советский физик-теоретик, лауреат Нобелевской премии.
[48] Фридман А.А. (1888-1925) – советский математик и геофизик; автор теории «нестационарной Вселенной».
[49] Ван – дер – Ваальс Я.Д. (1ё37 – 1923) – нидерландский физик.
[50] Метастабильными называются равновесные состояния с ограниченной устойчивостью. При отклонении от этого состояния вещество не стремится к нему обратно, а легко переходит в другое устойчивое состояние. Метастабильные состояния существуют ограниченное время.
[51] Ближний порядок — упорядоченность во взаимном расположении атомов или молекул в веществе, которая (в отличие от дальнего порядка) повторяется лишь на расстояниях, соизмеримых с расстояниями между атомами, то есть ближний порядок — это наличие закономерности в расположении соседних атомов или молекул.
[52] Средняя кривизна определяется через кривизну нормальных сечений. Нормальным сечением поверхности в некоторой точке называется линия пересечения этой поверхности с плоскостью, проходящей через нормаль к поверхности в рассматриваемой точке. Для сферы любое нормальное сечение представляет собой окружность радиуса R.
[53] Узкие цилиндрические трубки малого диаметра (< 1 мм) называются капиллярами.
[54] О́смос (от греч. ὄσμος — толчок, давление) — процесс односторонней диффузии через полупроницаемую мембрану молекул растворителя в сторону бо́льшей концентрации растворённого вещества (меньшей концентрации растворителя).
[55] Дальний порядок — упорядоченность во взаимном расположении атомов или молекул в веществе (в жидком или твёрдом состоянии), которая (в отличие от ближнего порядка) повторяется на неограниченно больших расстояниях.
[56] Примитивной ячейкой называется минимальный воображаемый объём кристалла, параллельные переносы (трансляции) которого в трёх измерениях позволяют построить трёхмерную кристаллическую решётку в целом.
[57] Браве О. (1811 – 1863) - французский кристаллограф.
[58] Дюлонг П.Л. (1785-1838) – французский физик и химик.
[59] Пти А.Т. (1791-1820) – французский физик.
[60]Более частным понятием является понятие агрегатного состояния вещества (лат. aggrego 'присоединяю') - состояние одного и того же вещества в определённом интервале температур и давлений, характеризующееся определёнными, неизменными в пределах указанных интервалов, качественными свойствами. Традиционно выделяют три агрегатных состояния: твёрдое тело, жидкость и газ. К агрегатным состояниям принято причислять также плазму.
[61] Самая низкая температура плавления у гелия : Тпл. = 1 К; самая высокая температура плавления из химически чистых элементов – у вольфрама: Тпл. = 3660 К = 33870С.
[62] Правило фаз Гиббса - закон термодинамики многофазных многокомпонентных систем, согласно которому число фаз z, сосуществующих в равновесии, не превосходит числа независимых компонентов п более чем на два: z  n + 2. В случае однокомпонентной системы z = 3.
n + 2. В случае однокомпонентной системы z = 3.
