 |
|
С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
Теорема 5. (признак сравнения). Пусть для членов рядов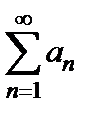 
и 
имеет место неравенство 
(для всех n или начиная с некоторого n). Тогда:
1) если сходится ряд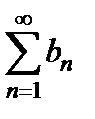 
, то сходится и ряд 
;
Если сходится ряд с большими членами, то сходится и ряд с меньшими членами. Обратное неверно.
2) если расходится ряд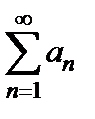 
, то расходится и ряд 
.
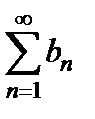Если расходится ряд с меньшими членами, то расходится и ряд с большими членами. Обратное неверно.
Пример 5. Исследуйте на сходимость ряд 
.
Решение. Так как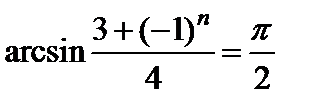 
при четных 
,
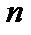и 
при нечётных 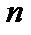, то числитель общего члена ряда принимает только два значения: 
и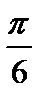 
. Можно записать следующую оценку: 
.
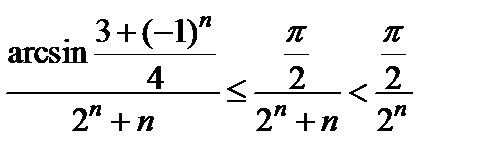Больший ряд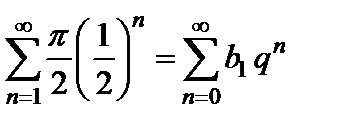 
составлен из членов геометрической прогрессии, где 
, 
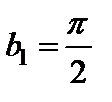и следовательно сходится. Тогда по признаку сравнения сходится и ряд с меньшими членами 
.
Теорема 6. (предельный признак сравнения). Пусть 
, 
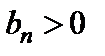, и существует предел 
. Тогда ряды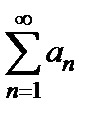 
и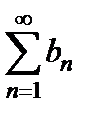 
ведут себя одинаково, т.е. сходятся или расходятся одновременно.
Теорема 7. (признак Даламбера). Пусть для ряда 
существует предел 
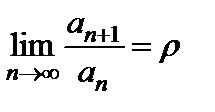. Тогда:
1) если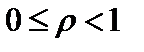 
, то ряд сходится;
2) если 
, то ряд расходится;
3) если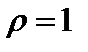 
, то требуется дополнительное исследование по другим достаточным признакам.
Пример 6. Исследуйте на сходимость ряд 
.
Решение.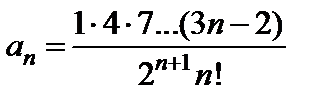 
, 
. Найдём
Следовательно, по признаку Даламбера данный ряд расходится.
Пример 7.Докажите справедливость равенства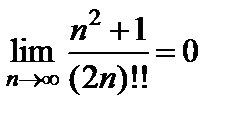 
.
Решение. Рассмотрим ряд 
и применим к нему признак Даламбера. Найдём предел:
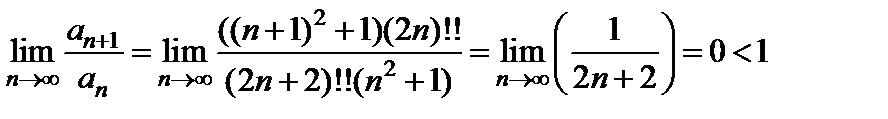. Следовательно, по признаку Даламбера ряд 
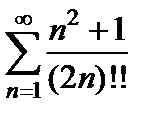сходится. Но тогда по необходимому признаку сходимости предел общего члена равен нулю: 
.
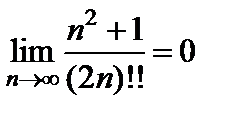Теорема 8. (радикальный признак Коши). Пусть для ряда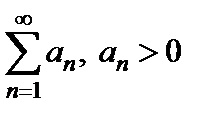 
существует предел 
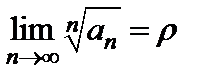. Тогда:
1) если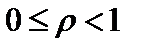 
то ряд сходится;
2) если , то ряд расходится;
3) если 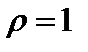, то требуется дополнительное исследование по другим достаточным признакам.
Пример 8. Исследуйте на сходимость ряд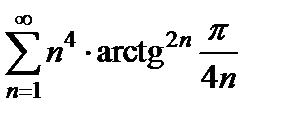 
.
Решение. Найдём предел:
.
Следовательно, по радикальному признаку Коши ряд сходится.
Теорема 9. (интегральный признак Коши). Пусть члены ряда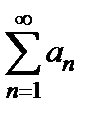 
имеют вид 
, где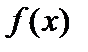 
– неотрицательная, монотонно убывающая функция на промежутке 
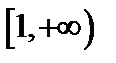. Тогда ряд 
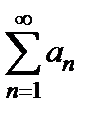сходится (расходится) тогда и только тогда, когда сходится (расходится) несобственный интеграл 
.
Пример 9. Исследуйте на сходимость обобщенно-гармонический ряд Дирихле 
.
Решение. Если 
то общий член ряда при 
стремится к бесконечности и ряд расходится по необходимому признаку. При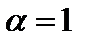 
имеем расходящийся гармонический ряд. При 
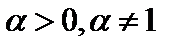положим 
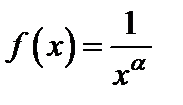. Функция 
непрерывна и монотонно убывает на промежутке 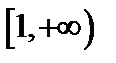. Известно, что несобственный интеграл 
сходится при 
и расходится при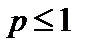 
. Следовательно, по теореме 3.5 ряд Дирихле сходится при 
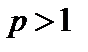и расходится при 
.
Пример 10. Исследуйте на сходимость ряд 
.
Решение. Непосредственное применение интегрального признака приводит к интегралу 
вычислить который довольно сложно. Поступим по-другому. Подберем ряд, эквивалентный данному в смысле сходимости. Рассмотрим ряд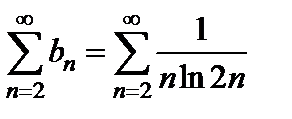 
.
Применим предельный признак сравнения. Вычислим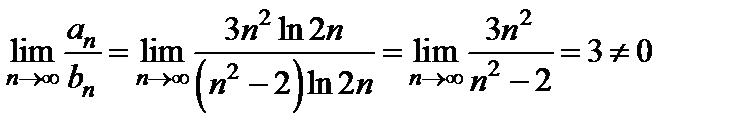 
. Следовательно, ряды 
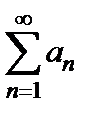и 
сходятся или расходятся одновременно по предельному признаку сравнения. Исследуем теперь ряд 
по интегральному признаку. Вычислим интеграл
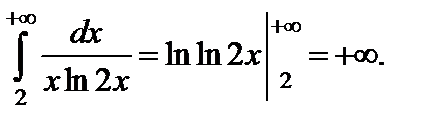
Несобственный интеграл 
расходится, следовательно по интегральному признаку ряд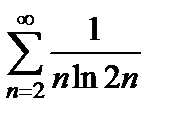 
расходится, тогда данный ряд 
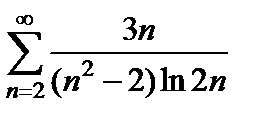также расходится по предельному признаку сравнения.
Рассмотрим еще один пример на применение предельного признака сравнения.
Пример 11. Исследуйте на сходимость ряд 
.
Решение. Рассмотрим ряд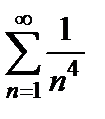 
. Это обобщенно-гармонический ряд Дирихле, он сходится, т.к. степень 
Применим предельный признак сравнения. Вычислим предел:
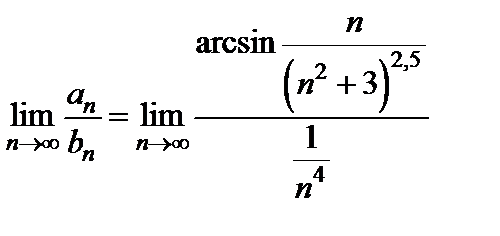. Так как при 
аргумент арксинуса
стремится к нулю,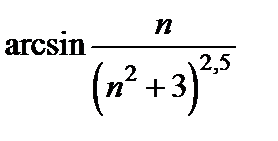 
является бесконечно малой величиной. По таблице эквивалентных бесконечно малых можно заменить в пределе 
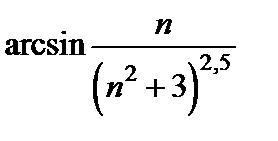на эквивалентную бесконечно малую 
:
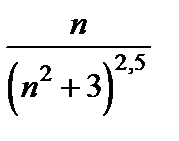Следовательно, ряды ведут себя одинаково. Так как ряд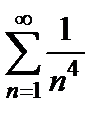 
сходится, то по предельному признаку сравнения будет сходиться и ряд 
.