 |
|
ЗНАКОЧЕРЕДУЮЩИЕСЯ РЯДЫ
Частным случаем знакопеременных рядов являются знакочередующиеся ряды, т.е. ряды вида
.
Теорема 11. (признак Лейбница). Пусть для ряда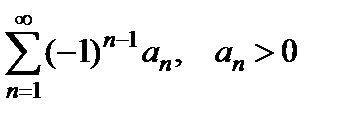 
выполнены условия:
1) 
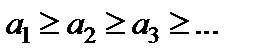(члены ряда не возрастают по абсолютной величине);
2) 
.
Тогда ряд 
сходится, причём его сумма не превосходит первого члена, т.е. 
.
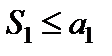Пример 12. Исследуйте на абсолютную и условную сходимость ряд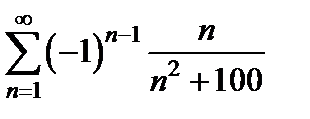 
.
Решение. Ряд из модулей имеет вид 
, он расходится по предельному признаку сравнения, т.к. эквивалентен в смысле сходимости гармоническому ряду 
: 
. Значит, данный ряд не сходится абсолютно.
Применим к исходному знакочередующемуся ряду признак Лейбница:
1) 
для всех 
, т.е. 
, 
.
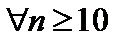2) 
.
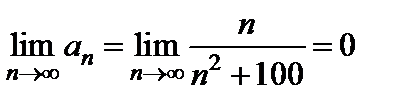Условия признака Лейбница выполняются при всех , следовательно,
остаток ряда 
сходится условно, а значит и сам ряд 
сходится условно.
Вычислим приближенно сумму данного ряда с точностью до 0,01. Заметим, что брать меньше 10 членов ряда нельзя, т.к. признак Лейбница начинает выполняться при . Запишем остаток ряда:
Под знаком модуля стоит сходящийся знакочередующийся ряд, для которого признаку Лейбница сумма не превосходит первого члена. Таким образом, 
, т.е. у знакочередующегося ряда остаток не превосходит по абсолютной величине первого отброшенного члена. Запишем неравенство 
. Оно будет выполняться при 
. Следовательно, для нахождения суммы данного ряда с точностью до 0,01, достаточно взять 98 первых его членов, т.е. 
.
6. СВОЙСТВА АБСОЛЮТНО И УСЛОВНО СХОДЯЩИХСЯ РЯДОВ
Теорема 12. Пусть ряды 
и 
сходятся абсолютно, и их суммы соответственно равны А и В. Тогда ряд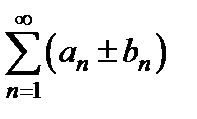 
сходится абсолютно, и его сумма равна 
.
Теорема 13. Если ряд 
сходится абсолютно, и его сумма равна А, тогда ряд 
, где c-const, сходится абсолютно, и его сумма равна 
.
Определение 4.2. Произведением рядов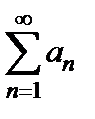 
и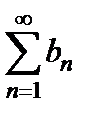 
называется ряд 
, где 
.
Теорема 14. Если ряд 
сходится абсолютно к сумме А, а ряд 
сходится условно к сумме В, то произведение этих рядов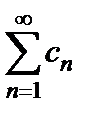 
сходится (необязательно абсолютно) к 
.
Теорема 15. Если ряд 
сходится условно, то оба ряда, составленные из положительных и отрицательных членов его, расходятся.
Известно, что сумма конечного числа слагаемых не зависит от перестановки слагаемых. Сохранится ли это свойство для бесконечного числа слагаемых?
Теорема 16. (Дирихле). Пусть ряд 
сходится абсолютно к сумме S. Тогда для любой перестановки членов ряда он останется сходящимся к сумме S.
Теорема 17. (Римана). Если ряд 
сходится условно, то для любого наперед заданного числа А существует такая перестановка членов ряда, что сумма будет равна А.