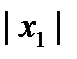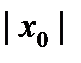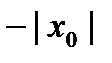Главная | Обратная связь

Свойства равномерно сходящихся рядов.

Теорема 5.2 (о непрерывности суммы ряда). Если: 1) все члены ряда 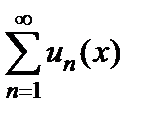являются непрерывными функциями; 2) ряд 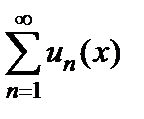сходится равномерно в области 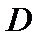, то сумма ряда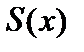 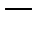непрерывная функция в области .

Теорема 5.3 (о почленном интегрировании ряда). Если члены ряда 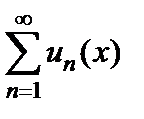являются непрерывными функциями, и ряд 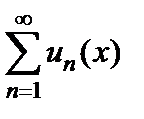сходится равномерно на к сумме , то его можно почленно интегрировать на любом 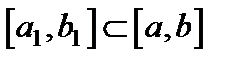, и справедлива формула

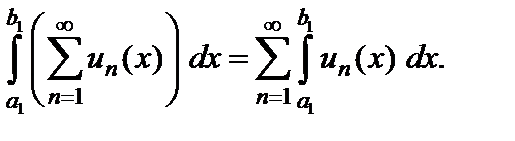
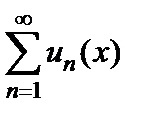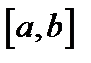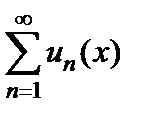Теорема 5.4 (о почленном дифференцировании ряда). Если члены ряда являются непрерывно-дифференцируемыми функциями на отрезке , ряд сходится на 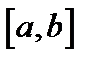, а ряд составленный из производных 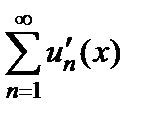сходится равномерно на 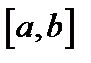, то ряд 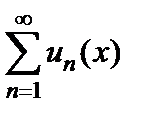сходится равномерно на 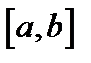, его сумма является непрерывно-дифференцируемой функцией, и ряд 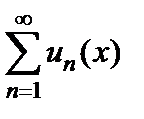можно почленно дифференцировать:

.

Пример 19. Докажите равномерную сходимость функционального ряда , .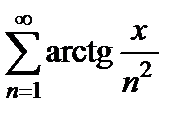

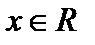Решение. Составим ряд из производных и докажем его равномерную сходимость по признаку Вейерштрасса. Заметим, что 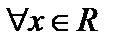, . Числовой знакоположительный ряд 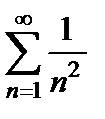сходится (ряд Дирихле, 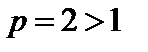). Следовательно, функциональный ряд 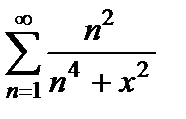по теореме 5.1 сходится равномерно при любом действительном 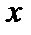. Тогда по теореме 5.4 исходный ряд сходится равномерно при любом 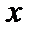, причём .

 

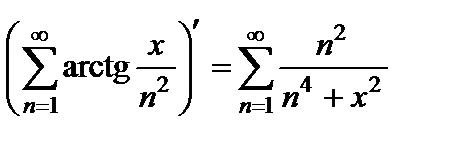Степенные ряды

Определение 6.1. Ряды вида

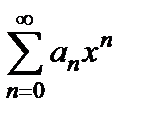, (6.1) (6.1)

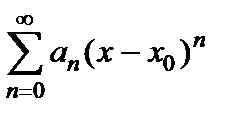, (6.2)

составленные из степенных функций, называются степенными. Действительные числа называются коэффициентами степенного ряда.

Степенной ряд (6.1) сходится по крайней мере в одной точке 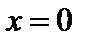, а ряд (6.2) – в точке 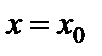. Так как заменой ряд (6.2) сводится к ряду (6.1), в дальнейшем рассматриваются ряды (6.1).

Теорема 6.1 (Абеля). Пусть степенной ряд 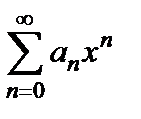сходится в некоторой точке . Тогда он сходится абсолютно в любой точке 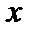, удовлетворяющей неравенству 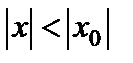, и сходится равномерно в области 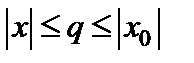. Если же ряд расходится в некоторой точке , то он расходится и во всех точках 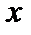, таких, что .

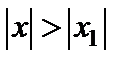абсолютно

На рисунке 2 приведена геометрическая иллюстрация теоремы Абеля.

сходится расходится расходится

рис. 2

Из рисунка 2 можно сделать заключение: областью сходимости степенного ряда (6.1) всегда является интервал, конечный или бесконечный, с центром в точке 0 или единственная точка 0.

Определение 6.1.Неотрицательное число 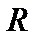такое, что степенной ряд (6.1) сходится в интервале и расходится при , называется радиусом сходимости степенного ряда, а интервал 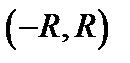- интервалом сходимости ряда. Если ряд (6.1) сходится в единственной точке 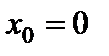, то для него . Если ряд сходится на всей числовой оси, то .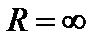

Для нахождения радиуса сходимости степенного ряда используют признак Даламбера и Коши.

, (6.3)

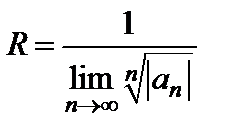. (6.4)

Эти формулы получены в предположении, что ряд (6.1) содержит все степени Если степени входят в ряд с пропусками, то непосредственное применение приведеннных формул для нахождения радиуса сходимости невозможно. В таких случаях определения области сходимости степенного ряда применяют непосредственно признак Даламбера или признак Коши.

Пример 20. Найдите область сходимости степенного ряда .

Решение. Данный степенной ряд содержит все степени 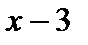, поэтому для нахождения его области сходимости можно применить формулу (6.3) и найти радиус сходимости. В нашем случае , .

.

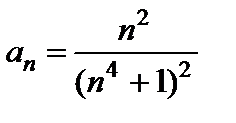Тогда интервалом сходимости степенного ряда будет являться интервал 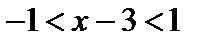или 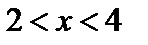. На концах интервала сходимости степенные ряды ведут себя по-разному. Поэтому проверим поведение данного ряда на концах интервала . Полученный промежуток и будет являться областью сходимости.

При 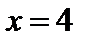получим числовой знакоположительный ряд . Чтобы определить его сходимость, применим предельный признак сравнения. Возьмем в качестве ряда сравнения ряд 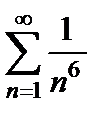и найдём

,

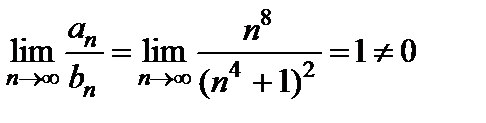где 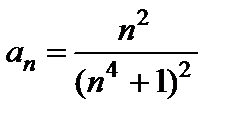. Следовательно, ряды и 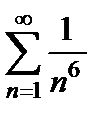ведут себя одинаково, т.е. сходятся или расходятся одновременно. Ряд 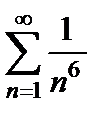сходится (ряд Дирихле, ), поэтому по предельному признаку сравнения сходится и ряд 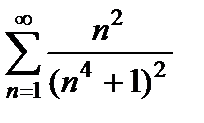. Таким образом, данный степенной ряд сходится при , т.е. на правом конце интервала сходимости.

При 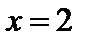получаем числовой знакопеременный ряд 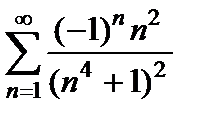, который сходится абсолютно, т.к. сходится ряд (см. выше). Т.е. на левом конце интервала сходимости степенной ряд также сходится.

Следовательно, областью сходимости степенного ряда 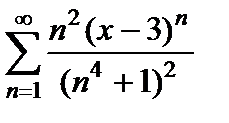является отрезок .

Пример 21. Найдите область сходимости степенного ряда .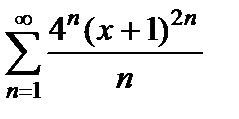

Решение. Заметим, что степенной ряд содержит не все степени 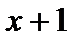, а только чётные, поэтому формулой (6.3) пользоваться нельзя. Найдём интервал сходимости, применяя непосредственно, например, признак Даламбера. Вычислим

.

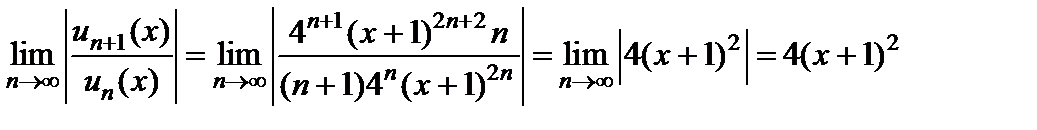По признаку Даламбера степенной ряд сходится, если . Найдём 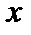из неравенства 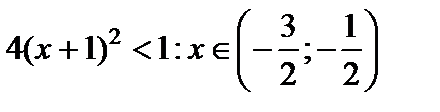. Исследуем поведение ряда на концах интервала сходимости. Подставим в данный степенной ряд и получим числовой знакоположительный ряд 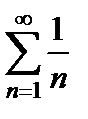. Это гармонический ряд, он расходится. Если 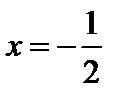, то приходим также к гармоническому ряду. Таким образом, на концах интервала сходимости степенной ряд расходится. Следовательно, областью сходимости является интервал .

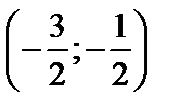Теорема 6.2. Сумма степенного ряда есть функция, непрерывная на любом от-резке из интервала сходимости.

Теорема 6.3. Степенной ряд можно почленно интегрировать на любом отрезке, целиком принадлежащем интервалу сходимости ряда. Степенной ряд можно почленно дифференцировать в интервале сходимости любое число раз. Ряды, полученные почленным интегрированием или дифференцированием степенного ряда, имеют тот же радиус сходимости, что и исходный ряд.

Пример 22. Найдите сумму ряда .

Решение. Интервалом сходимости данного степенного ряда является интервал . Составим ряд из производных: . Так как 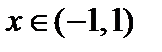, то члены ряда образуют бесконечно убывающую геометрическую прогрессию, поэтому 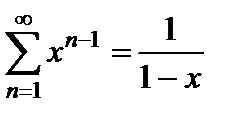. По теореме 6.3 степенной ряд можно почленно интегриро-вать на любом отрезке из интервала сходимости, т.е. из интервала 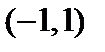. Проинтегрируем ряд 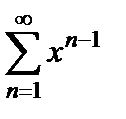в пределах от 0 до .

.

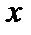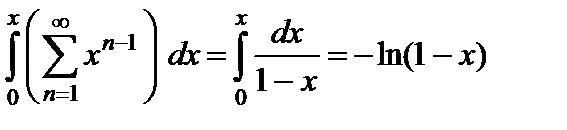С другой стороны

.

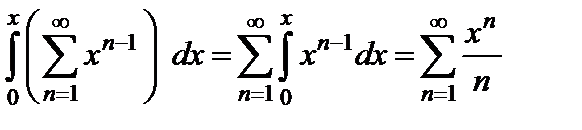Из приведенных преобразований делаем вывод, что 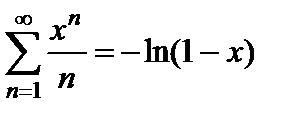.