 |
|
ОСНОВНІ ЗАЛЕЖНОСТІ І РОЗРАХУНКОВІ ФОРМУЛИ ДО РОЗДІЛУ І
1. Способи вираження складу фаз двокомпонентних систем “рідина – газ (пара)” наведені у табл. I.1.
Таблиця I.1
| Концентрація | Позначення концентрації компонента А | |
| у рідкій фазі | у газовій або паровій фазі | |
Мольна частка, 
| x | y |
Масова частка, 
| 
| 
|
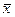
Відносна мольна концентрація (частка), 
| X | Y |
Відносна масова концентрація (частка), 
| 
| 
|
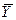
Об’ємна мольна концентрація, 
| 
| 
|
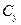
Об’ємна масова концентрація, 
| 
| 
|
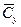
Формули для перерахунку концентрацій (у рідкій фазі) наведені в табл. I.2, де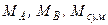 
– мольні маси компонентів у суміші, кг/кмоль; 
; 
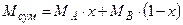– густина суміші, 
.
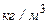Для ідеальних газів:
.
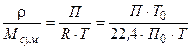Для газової (парової) фази справедливі такі самі співвідношення, але з заміною позначень Х на Y.
1.1. Вагові і мольні частки
Компоненти A, B, … , K, …, N, їх вагові частки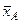 
, 
, …, 
, …, 
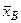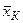і молекулярні маси компонентів дорівнюють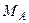 
, 
, …, 
, …, 
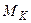. Кількість часток будь-якого компонента, наприклад, компонента K, що припадає на 1кг суміші, становить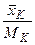 
.
Вміст цього компонента у суміші (в молекулярних частках)
.
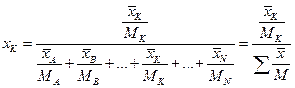Для зворотного перерахунку виразимо вагові частки 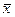компонентів через мольні частки 
.
Маси окремих компонентів, що містяться в 1кмолі суміші, становлять:
.
Відповідно вагова частка компонента: 
.
1.2. Об’ємні концентрації і вагові частки
Об’ємні концентрації компонентів: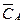 
, 
, …, 
, …, 
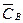, кг/м3.
Сума 
– маса суміші в 1м3 об’єму, або густина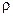 
суміші. Вагова частка будь-якого (наприклад, K-го) компонента виражається через його об’ємну концентрацію так:
.
1.3. Відносні концентрації
, 
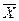– відносні вагові концентрації компонента, що розподіляється у взаємодіючих фазах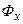 
і 
відповідно, тобто кількість його, що припадає на 1кг носія у кожній фазі.
Таблиця I.2
| Вираз концен-трації компо-нента А | x |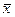
| X |
|
|
|
| x | – | 
або
| 
| 
| 
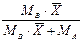
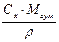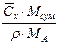або
| 
або
|
|
| 
| – | 
| 
| 
| 
|
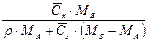
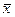
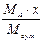
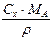
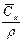
| X |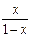 
| 
| – | 
| 
| 
|
|
| 
| 
| 
| – | 
| 
|
|
| 
| 
| 
| 
| – | 
|
|
| 
| 
| 
| 
| 
| – |
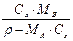
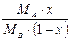
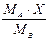
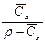
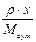
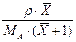
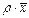
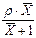
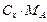
1.4. Відносні концентрації. Вагові і мольні частки
Нехай аміак поглинається водою. Відносна концентрація NH3 складає в рідкій фазі кг/кг води, в газовій фазі 
кг/кг повітря. Вагові концентрації через відносні розраховуються за залежностями:
; 
.
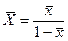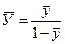2. Концентрація компоненту в газовій фазі може бути виражена також через його парціальний тиск. На основі рівнянь Клапейрона і Дальтона мольна (об’ємна) частка (y) будь-якого компонента суміші ідеальних газів дорівнює:
; (I.1.)
або
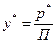, (I.1а)
де р – парціальний тиск компоненту газової суміші; 
– парціальний тиск поглинутого газу, який знаходиться в рівновазі з розчином;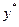 
– мольна (об’ємна) частка компонента суміші ідеальних газів, що є рівноважною з рідиною; 
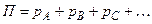– загальний тиск суміші газів або парів, що дорівнює сумі парціальних тисків всіх компонентів.
3. Закон Генрі:
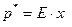, (I.2)
або
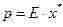, (I.2а)
де 
– мольна частка розчиненого газу в розчині, 
– концентрація газу в розчині (у мольних частках), що є рівноважним з газовою фазою, в якій парціальний тиск поглинутого компонента дорівнює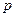 
; 
– коефіцієнт пропорційності, який називають коефіцієнтом, або константою Генрі.
Числові значення коефіцієнта Генрі для заданого газу залежать від природи поглинача і газу і від температури, але не залежать від загального тиску в системі.
Значення Е для водних розчинів деяких газів наведені в табл. 8Д.
Підставляючи значення парціального тиску з рівняння (I.2) в рівняння (I.1а), отримуємо:
. (I.3)
Або, підставляючи значення парціального тиску з рівняння (I.2а) в рівняння (I.1), отримуємо:
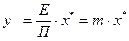, (I.3а)
де 
– безрозмірний коефіцієнт (коефіцієнт розподілення), сталий для даної системи “газ – рідина” при t = const та П = const. Також він є тангенсом кута нахилу лінії рівноваги.