Главная | Обратная связь

Модель идеального газа. Основное уравнение кинетической теории газов

Идеальный газ - теоретическая модель газа, в которой не учитывается взаимодействие частиц газа (средняя кинетическая энергия частиц много больше энергии их взаимодействия). Размеры молекул идеального газа малы по сравнению с расстояниями между ними (молекулы удалены в среднем друг от друга на расстояния, в десятки раз превышающие их линейные размеры). Суммарный собственный объем молекул такого газа мал по сравнению с объемом сосуда. Силы взаимодействия между молекулами настолько малы, что движение молекул от столкновения до столкновения происходит по прямолинейным отрезкам. Число ежесекундных столкновений молекул велико (в воздухе, например, при нормальных условиях, число столкновений в секунду порядка 10¹²). Средняя длина свободного пробега, т.е. среднее расстояние, пройденное молекулой от столкновения до столкновения, в сотни раз превышает их линейные размеры. Взаимодействия молекул идеального газа подчиняется законам упругого удара.

Различают идеальный классический и идеальный квантовый газ.

Свойства идеального классического газа описываются законами классической физики - уравнением Клапейрона и его частными случаями. Частицы идеального классического газа распределены, по различным состояниям, не зависимо друг от друга, и они различимы между собой. Распределение частиц идеального газа по энергиям описывается формулой распределения Больцмана.

Реальные газы хорошо описываются моделью идеального классического газа, если они достаточно разряжены.

Основное уравнение кинетической теории газов является важнейшим в молекулярно-кинетической теории; из него можно вывести все газовые законы, получить соотношения между энергией молекул и температурой и т.д.

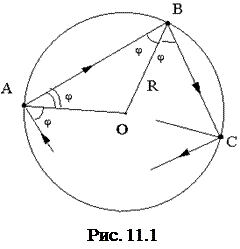
Возьмем сферический объем радиуса R, в котором находится N^' молекул. Молекулы ударяются друг о друга и о стенки сосуда; соударения молекул между собой приводят только к перераспределению скоростей и энергий между ними и не влияют на давление газа на стенки сосуда (рис. 11.1). Так как рассматривается идеальный газ, то объем самих молекул, и силы взаимодействия между ними на расстоянии не учитываются.

Давление газа на стенку сосуда, в общем случае, равно

, (11.2)

где 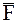- нормальная к площадке средняя сила, обусловленная ударами молекул.

Для определения давления воспользуемся вторым законом Ньютона в виде

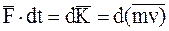, (11.3)

тогда

, (11.4)

следовательно, достаточно найти среднее значение изменения количества движения, которое молекулы сообщают единичной площади за время, равное единице, чтобы определить давление молекул на стенку сосуда.

Рассмотрим движение одной молекулы. Допустим, что она двигалась прямолинейно со скоростью v, затем ударилась о стенку под углом j, и отскочила от нее. Найдем перпендикулярную стенке проекцию импульса молекулы, переданного стенке при ударе. Проекция импульса, параллельная стенке, не влияет на давление, так как в среднем все эти проекции взаимно уничтожаются. Импульс равен изменению количества движения молекулы

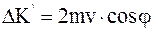. (11.5)

Путь, который молекула проходит от одного удара о стенку до другого, равен хорде, т.е. величине 2m∙v×cosj. Фактически молекула может пройти больший путь только в сильно разряженном газе. При обычных давлениях она столкнется на этом пути с другими молекулами и изменит направление движения. Но среди множества молекул, которые будут ударяться о стенку, всегда найдется какая-то молекула, обладающая такой же скоростью и направлением движения, какими обладала бы первая молекула, если бы она прошла путь, равный хорде. Поэтому можно рассматривать движение молекулы (выбранной произвольно) так, как будто она проходит путь равный хорде без столкновений с другими молекулами.

Число ударов молекулы о стенку за одну секунду равно отношению скорости молекулы к пути, проходимому молекулой от одного удара о стенку до другого

. (11.6)

Сумма импульсов одной молекулы, сообщенных стенке за секунду равно

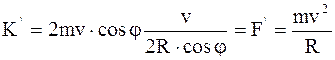, (11.7)

а сумма импульсов всех молекул за секунду

. (11.8)

Давление газа найдем, разделив силу на площадь

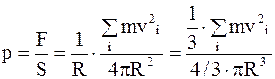, (11.9)

где 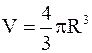- объем газа.

Перепишем равенство (11.9) в виде

, (11.10)

где E^' - кинетическая энергия одной молекулы.

Умножим и поделим правую часть (11.10) на N^' - число молекул в объеме V, получим

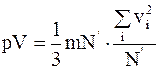, (11.11)

или

, (11.12)

где 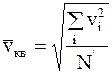- средняя квадратичная скорость.

Уравнение (11.12) является основным уравнением молекулярно-кинетической теории. Его можно переписать в виде

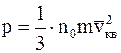, (11.13)

где n₀ = N^'/V - число молекул в единице объема.

Уравнение (11.13) называют основным уравнением молекулярно-кинетической теории газов для давления. Его называют уравнением Клаузиуса. Сделав некоторые преобразования из (11.13) можно получить

(11.14)

где n₀ = N^'/V - число молекул в единице объема;

- средняя кинетическая энергия поступательного движения молекул газа;

k - постоянная Больцмана.