Главная | Обратная связь

Основное уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)

Моли разных газов (при неизменных давлении p и температуре Т) занимают равные объёмы, следовательно, для одного моля любого газа

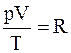, (11.34)

где R - универсальная газовая постоянная.

Так как в формуле (11.34) для одного моля B×m = B×m = R, то B = R/m, следовательно, для произвольной массы газа

или . (11.35)

Уравнение (11.35) носит название уравнения Менделеева-Клапейрона. Оно является основным уравнением состояния идеального газа.

Для одного моля идеального газа основное уравнение может быть записано так

. (11.36)

11.2.2.6. Закон Авогадро

Запишем основное уравнение молекулярно-кинетической теории для двух газов, занимающих одинаковые объемы при одинаковых температурах и давлениях в виде

, (11.37)

, (11.38)

где и - кинетические энергии молекул газов, которые ввиду равенства температур одинаковы.

Приравняв правые части выражений (11.37) и (11.38), сократив числовые коэффициенты и кинетические энергии, получим

N₁ = N₂, (11.39)

т.е. в одинаковых объемах при одинаковых температурах и давлениях содержатся одинаковые количества молекул.

Формула (11.39) отображает закон Авогадро.

Число молекул в единице количества вещества (в одном моле) называется числом Авогадро, числовое значение которого N_A = 6,023×10²³ моль^-1.

Закон Дальтона

Из основного уравнения молекулярно-кинетической теории давление газа определяется соотношением

, (11.40)

где n₀ = N^'/V – число молекул в единице объема;

<E^'> - средняя кинетическая энергия молекул газа.

Для смеси нескольких газов общее количество молекул газа в единице объема равно сумме количеств молекул в единице объема отдельных газов

n = n₀₁ + n₀₂ + ….. + n_0n. (11.41)

Поскольку все газы в смеси находятся при одинаковой температуре, средние кинетические энергии их молекул одинаковы:

<E^'₁> = <E^'₂> = ….. = <E^'_n> = <E^'>. (11.42)

Подставив (11.41) в (11.40) и учитывая (11.42), получим

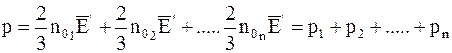, (11.43)

т.е. «Давление смеси газов равно сумме парциальных давлений, т.е. тех давлений, которые имел бы каждый из входящих в смесь газов, если бы в объеме, занятом смесью, находился он один».

Формула (11.43) отображает закон Дальтона.

Хотя закон Дальтона справедлив для смеси идеальных газов, но он очень хорошо выполняется в широком диапазоне давлений и температур реальных газов, и поэтому имеет большое практическое значение.