Главная | Обратная связь

Вывод основных газовых законов молекулярно кинетической теории

Из основного уравнения молекулярно-кинетической теории газов (11.12) можно вывести все газовые законы, установленные экспериментально.

11.2.2.1. Закон Бойля-Мариотта

В основном уравнении для данной массы газа величины N^', m и │v_кв│ - постоянные при неизменной температуре (скорость молекул пропорциональна корню квадратному из абсолютной температуры). Таким образом, правая часть уравнения является произведением постоянных величин, отсюда: «Для данной массы газа при неизменной температуре произведение его давления на объем величина постоянная». Данное утверждение и является законом Бойля-Мариотта

p×V = const. (11.15)

В термодинамике процесс, происходящий при постоянной температуре, называется изотермическим. Графически он изображается в координатах p, V изотермой (рис. 11.2).

Закон Гей-Люссака

Запишем основное уравнение молекулярно-кинетической теории для двух состояний одной и той же массы газа при одинаковых давлениях, но разных температурах

, (11.16)

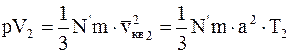, (11.17)

где квадрат средней квадратичной скорости v_кв заменен на a²×T (a - коэффициент пропорциональности; T - абсолютная температура).

Разделив (11.16) на (11.17), получим

, (11.18)

т.е. для данной массы газа при постоянном давлении их объемы относятся как абсолютные температуры. Или «Для данной массы газа при постоянном давлении отношение объема к абсолютной температуре остается величиной постоянной»:

. (11.19)

Формулы (11.18) и (11.19) отображают закон Гей-Люссака.

В термодинамике процесс, происходящий при постоянном давлении, называется изобарическим.

Экспериментально установлено, что в этом случае объем газа изменяется по закону (при m = const, p = const)

V_t = V₀×(1 + at), (11.20)

где a - коэффициент объёмного расширения - величина, которая показывает, как изменилась каждая единица начального объёма газа (при 0 ⁰С) от нагревания его на один градус при постоянном давлении

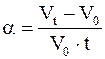. (11.21)

Такой процесс в координатах V, t он изображается изохорой (рис. 11.3).

Закон Шарля

Если данную массу газа нагреть при постоянном объеме от температуры T₁ до температуры T₂, то основное уравнение молекулярно кинетической теории для этих двух состояний будет иметь вид

, (11.22)

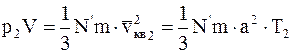. (11.23)

Разделив (11.22) на (11.23), получим

, (11.24)

т.е. для данной массы газа при постоянном объеме их давления относятся как абсолютные температуры. Или: «Для данной массы газа при постоянном объеме отношение давления к абсолютной температуре остается величиной постоянной»

. (11.25)

Формулы (11.24) и (11.25) отображают закон Шарля.

В термодинамике процесс, происходящий при постоянном объеме, называется изохорическим.

Давление данной массы газа при изохорическом процессе изменяется по закону (при m = const, V = const)

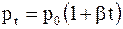, (11.26)

где b - термический коэффициент давления, который показывает, на какую часть изменилась каждая единица начального давления газа (при 0 ⁰С) от нагревания его на один градус при постоянном объёме

. (11.27)

Графически в координатах p, t такой процесс изображается изобарой (рис.11.4).

Так как a = b, то все изобары и изохоры пересекают ось "t" в одной и той же точке. Если начало отсчёта температур сместить в эту точку, то мы перейдём к другой температурной шкале - шкале Кельвина (абсолютной шкале температур). При этом между температурой по шкале Кельвина и температурой по шкале Цельсия существует связь

T = t + 273,15. (11.28)

11.2.2.4. Объединенный газовый закон Мариотта - Гей-Люссака

Запишем основное уравнение молекулярно-кинетической теории для данной массы газа в двух состояниях при изменении температуры, давления и объема

, (11.29)

. (11.30)

Разделив (11.29) на (11.30), получим

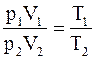, (11.31)

т.е. для данной массы газа произведение давления на его объем относятся как абсолютные температуры. Или «Произведение давления газа на его объем, деленное на абсолютную температуру, для данной массы газа остается величиной постоянной»

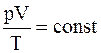. (11.32)

Формулы (11.31) и (11.32) отображают объединенный газовый закон Мариотта-Гей-Люссака.

Оказывается, что при изменении массы газа, постоянная величина в этом законе изменяется пропорционально массе, т.е.

, (11.33)

где "B" принимает для различных газов различные значения.

Уравнение (11.33) носит название уравнение Клапейрона.