Главная | Обратная связь

Перший закон термодинаміки

(закон збереження енергії для систем, в яких основну роль грають теплові процеси)

Якщо термодинамічній системі надати зовні деяку кількість теплоти 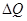і виконати на цією системою роботу 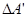зовнішніми силами, то внутрішня енаргія цієї системи зміниться на величину , яка чисельно дорівнює:

(11)

Робота 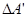зовнішніх сил над системою дорівнює по величині і протилежна за знаком деякій роботі , яка здійснюється системою проти зовнішніх сил, тобто:

З урахуванням цього, рівняння (11) запишемо:

(12)

Для нескінченно малої зміни стану системи можна записати:

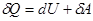(13)

Дане рівняння – математичний запис першого початку термодинаміки.

За першим законом термодинаміки: теплота, надана системі витрачається на зміну внутрішньої енергії системи і на здійснення системою роботи проти зовнішніх сил.

Для визначення кругових процесів, коли система набуває ряд змін і повертається у початковий стан (положення):

Тому перший закон термодинаміки:

Це твердження (перший закон термодинаміки) було сформоване Гальм-Гольцем у 1747 році.

Якщо система здійснює круговий процес, то повна кількість теплоти, яка надається системі, дорівнює здійсненій в ній роботі. З рівняння (13) випливає, що у випадку кругових процесів:

Перший початок термодинаміки стверджує: неможливий процес, єдиним результатом якого було б виконання роботи без яких-небудь змін в інших тілах. Іншими словами, неможливий вічний двигун першого роду.

Усі формулювання першого закону термодинаміки виражають закон збереження енергії. У випадку теплового процесу для однорідних тіл, здатних виконувати роботу при зміні об’єму, запишемо:

(14)

Якщо враховувати рівняння (10), запишемо:

(15)

 

Ізопроцеси в ідеальних газах

А)Ізотермічний

Ізотермічний процес здійснються при сталій температурі системи (Т=const), при m=const, n=const. При 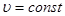, рівняння Менделєєва-Клайперона запишемо:

pV=const (16)

 

Ізотермічні процеси відбуваються досить повільно. При цьому поняття температури не втрачає сенсу. Стискаємість ідеального газу при T=const характеризується ізотермічним коефіцієнтом стискаємості χ, який визначається як відносна зміна об’єму, що зумовлює зміну тиску на одиницю:

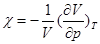(17)

де V – початковий об’єм

- зміна об’єму, яка зумовлює зміну тиску на

Знайдемо коефіцієнт χ для ідеального газу. Продиференціювавши (16) при T=const, дістанемо:

звідси:

(18)

тобто при , тоді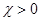

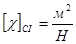
Для реазізації ізотермічного процесу треба забезпечити ідеальний тепловий контакт між газом і термостатом (тілом, що має сталу температуру).

Оскільки , то перший закон термодинаміки для ізотермічного процесу:

(19)

Роботу визначають:

(20)

З урахуванням (20), рівняння (19) перепишемо так:

(21)

Б)Ізобарний

Ізобарний процес відбувається в системі при сталому тиску (P=const).

Такий процес можна здійснити, коли газ, наприклад, міститься в циліндрі з рухомим поршнем. Зміна температури газу в такому циліндрі зумовлює переміщення порщня, тобто зміну об`єму. Тиск при цьому залишається сталим:

(22)

- рівняння ізобарного процесу,виражає закон Гей-Люссака:

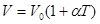
- коефіцієнт об’ємого розширення газу

= 0,003661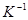

Аналогічно, коефіцієнт χ:

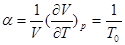
Розглянемо графік p(V): газ, поміщений в циліндр із вільно-рухомим поршнем, під час нагрівання 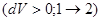або під час охолодження здійснює ізобарний процес.

Елементарна робота:

(23)

є повним диференціалом деякої функції. Оскільки p=const, то робота є однозначною функцією параметрів початкового і кінцевого станів системи (парметр V). Звідси:

(24)

Диференціюючи рівняння Менделєєва-Клайперона при сталому тиску, одержимо:

Тоді:

Кількість теплоти, якою газ обмінюється в ізобарному процесі при незалежності від температури:

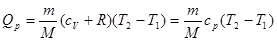(25)

Кількість теплоти йде не тільки на збереження внутрішньої енергії, а йна виконання роботи щодо розширення газу:

(26)

В)Ізохорний

Ізохорний процес відбувається при сиалому об’ємі газу (V=const):

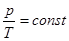(27)

- рівняння ізохорного процесу

За законом Шарля, рівняння ізохорного процесу також можна записувати у вигляді:

- термічний коефіцієнт тиску ( )

Аналогічно до коефіцієнту :

Зв’язок між коефіцієнтами :

Робота в ізохорномк процесі дорівнює нулю:

(28)

Тоді рівняння першого закону термодинаміки:

(29)

Г)Адіабатичний

Адіабатичний процес відбувається без теплообміну з навколишнім середовищем.

Адіабатне розширення або стискання газу можна здійснити, помістивши його в циліндр із нетеплопровідними стінками і поршнем, і досить повільно переміщуючи поршень назовні або всередину циліндра. Стан системи при адіабатичному процесі можна змінити тільки за допомогою зміни зовнішніх парамеирів.

Для цього процесу характерним є те, що газ увесь час залишається під зовнішнім тиском, який дорівнює пружності газу. Другою умовою адіабатичного процесу є теплоізольованість газу від навколишнього середовища.

Для адіабатичного процесу рівняня першого закону термодинаміки має вигляд:

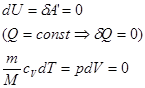(30)

Виразимо P через V і T з рівняння стану ідеального газу:

Підставимо в попереднє рівняння і скоротимо на відмінний від нуля множник :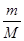

Розділимо обидві частини рівняння на :

Це співвідношення можемо записати у вигляді:

Звідси слідує, що при адіабатичному процесі:

Проінтегрувавши і підставивши, одержимо:

(31)

- рівняння адіабатичного газу в змінних T і V:

враховуючи, що величини M,m і R – сталі:

(32)

- рівняння адіабатичного ідеального газу в змінних P і V (рівняння Пуассона).

При ізотермічному процесі (pV=const), тиск газу зменшується обернено-пропорційно об’єму в першому степені. При адіабатичному розширенні тиск зменшується обернено-пропорційно . Хід адіабати крутіший порівняно з ізотермою. Фізично це пояснюється тим, що при адіабатичному розширенні зменшення тиску зумовлене не тільки збільшенням об’єму, а й зменшенням температури.

Виведемо формули для розрахунку роботи при адіабатичному процесі: з попередніх викладок для 1 моль ідеального газу:

(33)

Оскільки

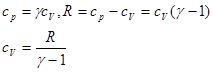(34)

то:

- показник адіабати

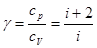(35)

Графічно робота зображено площею заштрихованої трапеції.

 

 

Другий закон термодинаміки

 

1. Кругові процеси

2. Цикли Карно

а) Прямий обернений цикл Карно

б) Обернений рівновісний цикл Карно

в) Необернений цикл Карно

3. Нерівність Клаузіуса

4. Ентропія та її властивості

5. Другий закон термодинаміки

Кругові процеси

Щоб описати усі термодинамічні процеси, першого закону термодинаміки недостатньо. Процес самостійної передачі енергії у вигляді теплоти від менш нагрітого тіла до більш нагрітого тіла не протирічить першому закону термодинаміки, тобто перший закон термолинаміки не виключає можливості такого процесу, результатом якого було б перетвореня теплоти, що отримана системою в еквівалентній їй роботі. Можна було б побудувати двигун, який би здійснював роботу за рахунок охолодження одного джерела теплоти іншим, наприклад, за рахунок внутрішньої енергії Світового океану.

Це був би вічний двигун другого роду. Аналіз кругових процесів, що лежать в основі всіх теплових двигунів показує, що побудуавти такий двигун – неможливо. Це і є основою другого закону термодинаміки.

Кругові процеси – процеси, в результаті яких системи проходячи ряд проміжних станів повертається в початковий стан – круговий цикл. Ці кругові процеси різні: наприклад, термодинамічний процес називається оберненим, якщо він допускає повернення системи з кінцевого стану в початковий стан без того, щоб в навколишньому середовищі залишились які-небудь зміни. При цьому, проміжні зміни допускаються, але повернення у початковий стан системи і в навколиишнє середовище обов’язкове. Всі інші процеси називаються необерненими.

Якщо система з кінцевого стану В може повертатися в початковий стан А без різниці, таким чином не потребуючи, щоб вона обов’язково проходила ту чи іншу послідовність станів, що і в прямому процесі ( ), то такий процес називається оберненим в широкому змісті слова. Якщо при поверненні системи вона обов’язково повинна проходити ту саму послідовність, що і в прямому процесі , то такий процес - обернений у вузькому змісті слова. Усі квазірівновісні (квазістатичні) процеси є оберненими у вузькому змісті слова.

У випадку обернених процесів над газом, наприклад при розширенні від , виконується робота і при стисканні газу від до , над газом виконується робота . Якщо процес вести за годинниковою стрілкою, то результат роботи – позитивний А>0 і при цьому за першим законом газ в результаті кругового процесу отримує кількість теплоти 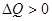. Такий процес називається прямим процесом. Якщо процес вести проти годинникової стрвілки, то повна робота циклу А<0 і газ буде віддавати теплоту . Такий цикл називається оберненим.

 

Цикли Карно

Прямий обернений цикл Карно

Цикл Карно дозволяє підійти до поняття коефіцієнта дії теплової машини.

Схема роботи ідеальної теплової машини, щл працює по циклу Карно:

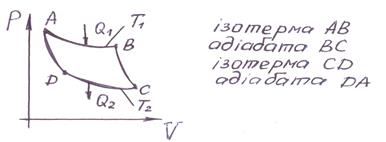
1. Нагрівач отримує теплоту , і газ під поршем починає розширюватися так як (ізотерма АВ). Так як процес рівновісний, то температура газу дорівнює температурі нагрівача.

2. Газ теплоізольований і починає адіабатично розширюватись до яка дорівнює температурі холодильника (адіабата ВС).

3. Газ ізотермічно стискається, віддаючи холодильнику теплоту .

4. Газ адіабатно стискається, нагріваючись до температури нагрівача (адіабата DA).

Знайдемо роботу, яку здійснює ідеальний газ в даному циклі. Так як тепловий цикл – круговий, то повна зміна внутрішньої енергії газу дорівнює нулю ( ). Тоді перший закон термодинаміки для робочого тіла (газу) в циклі Карно має вигляд:

(1)

при цьому слід пам’ятати, що:

Роботу цикла можна виразити як суму робіт окремих процесів:

Так як сумарна робота адіабатичного розширення і стискання газу в даному циклі чисельно дорівнює нулю, тому:

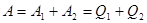(2)

А – корисна робота циклу

Так як , то з рівняння (2) слідує, що ця робота і менша від тієї кількості теплоти, що підводиться до нагрівача. Частина енергії віддається холодильнику у вигляді теплоти . Данний висновок справедливий для будь-якого кругового процесу. Величину відношення роботи до кількості теплоти позначають - термічний коефіцієнт теплового двигуна:

Для нашого оберненого циклу Карно:

(3)

Формула (3) не меє жодних данних про властивості робочого тіла і про будову теплової машини, тобто звідси випливає, що ККД усіх обернених машин, що працюють в ідеальних умова, тобто при одній і тій самій температурі нагрівача 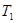і темперетурі холодильника буде однаковим і визначатиметься тільки температурами нагрівача і холодильника. Дане твердження носить назву теореми Карно, яка є основою встановлення термодинамічної шкали температур.

З рівняння (3) випливає:

Таким чином, щоб порівняти температури двох тіл , потрібно здійснити оберненеий цикл Карно, в якому ці тіла використовуються у вигляді нагрівача і холодильника і порівняти теплолу .

Термодинамічна шкала не зв’язана з властивостями термодинамічного тіла і в цьому є її досягнення. Але внаслідок необерненості реальних термодинамічних процесів, такий спосіб порівняння температур практично не виконується і має лише принципіальне значення.

Обернений рівновісний цикл Карно

В оберненому циклі Карно теплота відводиться від газу в процесі ізотермічного стискання при температурі 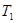, а кількість теплоти навпаки підводиться до газу в процесі ізотермічного розширення при . Тоді результуюча робота , тобто результуюча робота виконується зовнішнім середовищем над газом.

Даний результат справедливий для будь-якого оберненого циклу, таким чином за рахунок здійсненої роботи зовнішніми силами над робочим тілом, можна переносити енергію у вигляді теплоти від менш нагрітого тіла до більш нагрітого тіла. Даний метод використовується в холодильній техніці. Холодильна техніка буде тим більш економічною, чим менша буде робота , яка витрачається зовні на відведення від холодильного тіла теплоти .

З рівняння, що і з умови, що , знаходимо, що:

(4)

Необернений цикл Карно

Нехай необерненість циклу обумовлена тим, що теплообмін між робочим тілом, нагрівкчем та холодильником відбувається при кінцевих різницях температур нагрівача і робочого тіла. Тобто:

Необернений цикл неможливо характеризувати в будь-який момент часу заданими параметрами, але можливо деяким чином змінити параметри системи і розглянути цикл подібно до оберненого.

Так, при розширенні газу, що контактує з нагрівачем, його температура буде менше, ніж температура нагрівача, а при швидкому стисканні газу, що контактує з холодильником, температура газу в середньому буде більшою, ніж температура холодильника. Звіди випливає, що при знаходженні коефіцієнта корисної дії необерненого циклу Карно температуру 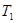необхідно замінити на температуру , а температуру - на . Тоді ККД необерненого циклу буде визначатися як:

(5)

Можна показати, що ККД необерненого процесу майже завжди менше ніж ККД оберненого циклу Карно. Таким чином:

(6)

- екстримальні значення температури нагрівача і холодильника, які отримали загальні назви джерел теплоти.