 |
|
Енергія Гальм-Гольца
Згідно рівнянь першого закону термодинаміки 
, робота, що виконується за рахунок теплоти при оберненому процесі:
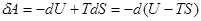(7)
Функція
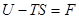(8)
називається енергією Гальм-Гольца або вільною енергією.
Відповідно до (7) і (8), при оберненому ізотермічному процесі робота дорівнює зменшенню енергії Гальм-Гольца:
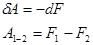(9)
Зрівнюючи (9) і (5), можна побачити, що при ізотермічних процесах вільна енергія грає таку саму роль, як і внутрішня енергія при адіабатичних поцесах.
У випадку необернених ізотермічних процесів:
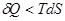
і робота:
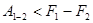(10)
З цього слідує, що зменшення енергії Гальм-Гольца характеризує верхню границю роботи, яку може здійснити система при ізотермічному процесі.
Якщо продиференціювати рівняння (8) з урахуванням рівняння першого закону термодинаміки, отримаємо:
dF=-SdT-pdV (11)
За рівняннями (2) і (3) і на основі (11) знаходимо, що:
(12)
З даних двох рівнянь слідує, що природніми змінними енергії Гальм-Гольца є змінні температури і об’єми.
Поділимо рівняння першого закону на dt і отримаємо:
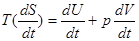(13)
При умові, що T=const, V=const, отримаємо, що :
(14)
З рівняння (14) слідує, що необернений процес, що протікає при постійних температурі і об’ємі супроводжується зниженням енергії Гальм-Гольца і рівновісним при цих умовах є стан з мінімальною енергією Гальм-Гольца.
Ентальпія
Для процесів, які протікають при тостійному тискові (p=const), перший закон термодинаміки можна записати у вигляді:
або:
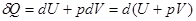
Величина (U+pV) дорівнює H:
U+pV=H (15)
і це є функція зміни стану, яка називається ентальпією. Використовуючи цю функцію, знаходимо, що кількість теплоти, отриманої тілом в ході ізобарного процесу, чисельно дорівнює:
(16)
Якщо продиференціювати рівняння (15) з урахуванням другого закону термодинаміки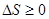 
, то отримаємо:
dH=dU+pdV+Vdp=TdS-pdV+pdV+Vdp=TdS+Vdp
Звідси витікає, що ентальпія – термодинамічна функція змінних ентропії і тиску.Її частинні похідні:
(17)
З урахуванням (16), теплоємність при p=const:
(18)
Співставляючи властивості внутрішньої енергії і ентальпії, неважко зрозуміти, що при p=const ентальпія володіє властивостями, аналогічними до тих, що має внутрішня енегрія при V=vonst.
Потенціал Гіббса
Енергією Гіббса називається функція стану, що визначається рівнянням:
G=H-TS=U+pV-TS (19)
Повний диференціал енергії Гіббса визначається як:
Така як dU=TdS-pdV, то нотенціал енергії Гіббса:
dG=Vdp-SdT
Тобто природними змінними для функції енергії Гіббса є тиск і температура (p i T), а частинні похідні цієї функції:
(20)
Якщо температура T і тиск p залишаються сталими, то відповідно до рівняння (13) можна записати:
(21)
З рівняння слідує: якщо необхідний процес буде проходити при посійному тискові p=const і постійній температурі T=const, то це буде супроводжуватися зменшенням енергії Гіббса.
В стані рівноваги енергія Гіббса буде мінімальною.