 |
|
Закон розподілу Больцмана
Розглянемо розподіл мікрочастинок за енергіями на прикладі ідеального газу, що знаходяться в полі тяжіння: нехай сили поля напрямлені вздовж осі z.
Тиск газу в різних точках вздовж цієї осі буде різним. Виберемо дві площини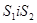 
, причому 
. Ці площини орієнтовані перпендикулярно до осі z і знаходяться на відстані dz одна від одної. Якщо тиск газу на обох площинах буде чисельно дорівнювати p i p+dp, то різниця тисків dp чисельно дорівнює сумарній силі, що діє на частинки газу, що знаходяться в об’ємі даного паралелепіпеда з основою S і висотою dz відносно до площі даної основи:
n – конценрація молекул в даному об’мі
- сила, що діє на 1моль в точці з координатою z
Дана сила пов’язана з потенціальною енергією молекули співвідношенням:
Таким чином, додатковий тиск dp чисельно дорівнює:
Приймаючи температуру ідеального газу у всіх точках однаковою, на основі рівняння Менделєєва-Клайперона, знаходимо, що:
Співставляючи два останні рівняння:
Проінтегрувавши і пропотенціювавши даний вираз, отримаємо:
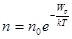(1)
Рівняння (1) називають законом розподілу Больцмана.
В даному рівнянні 
і n- концентрації молекул газу в стані з відповідно прийнятою нульовою потенціальною енергією і деякою 
в стані 1.
Рівняння може бути отримане з більш загальних міркувань. Воно має універсальний характер, бо використовується для будь-яких систем з мікрочастинок, що знаходяться в різних потенціальних полях. Наприклад, для поля тяжіння Землі на великій висоті:
(2)
Для двох різних станів з потенціальними енергіями 
, отримаємо:
(3)
Так як тиск газу пов’язаний з концентрацією молекул рівнянням p=nkT, то на основі рівняння (2), запишемо:
(4)
Тиск p і тиск 
:
- тиск на поверхні Землі
p - на висоті z над Землею
- молярна маса газу
Рівняння (4) – барометрична формула.