 |
|
Закон розподілу Максвела
Теплова або середня квадратична швидкість 
представляє собою середню характеристику теплового руху усієї сукупності мікрочастинок. В дійсності, всі мікрочастинки рухаються з різними швидкостями і можна поставити питання про розподіл мікрочастинок за швидкостями.
Максвел вирішив цю задачу про розподіл молекул ідеального газу за швидкостями постійного руху в стані теплової рівноваги. Він показав, що вірогідність того, що деяке число молекул dN із загального числа молекул N володіє швидкостями, що лежать у інтервалі від 
до 
. Виражається дана вірогідність відношенням:
(5)
f(v) - функція розподілу молекул за швидкостями
dv - інтервал швидкостей, що розглядається
Вигляд функції можна встановити на прикладі руху молекул ідеального газу в однорідному полі тяжіння. Спочатку розглянемо закон розподілу молекул по значенням вертикальної складової швидкості. Число молекул , що знаходяться в безкінечно тонкому шарі газу на висоті z, товщина dz:
n(z) – концентрація молекул газу на висоті z.
Рухаючись як вільні, дані молекули через деякий інтервал часу перейдуть на висоту 
і займуть шар 
. При цьому, їх швидкості будуть лежати в інтегралі від 
до 
, але одне і те ж число молекул. Якщо прийняти, що 
, то незмінність числа цих молекул виражається:
(6)
- концентрація молекул газу на висоті .
При русі в полі тяжіння горизонтальні складові швидкості 
не будуть змінюватись, а зміна визначається законом збереження енергії, згідно якого:
Якщо продиференціювати це рівняння, при вибраних сталих значеннях 
, отримаємо:
За час dt молекула на висоті z пройде шлях 
, а на висоті , пройде шлях 
Якщо виключимо елементарний час dt, то:
(7)
Перемножимо почленно рівняння (6) і (7) і знайдемо:
Із урахуванням останнього виразу, рівняння (5) спрощується і приймає вигляд:
Використовуючи закон Больцмана у вигляді рівняння (2), отримаємо:
На основі закону збереження і перетворення енергії, знаходимо, що:
Тоді:
Звідси слідує, що:
(8)
В стані теплової рівноваги рух молекул газу буде рівновигідним по всіх напрямках.
Так як вірогідність складної події, яка складається з незалежних подій, рівна добутку вірогідностей цих подій, то повні функція розподілу молекул за швидкостями буде мати вигляд:
Тоді:
(9)
З урахуванням рівняння (9), запишемо рівняння (5):
(10)
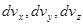- об’єми нескінчено малого паралелепіпеда, що побудований в координатній системі простору швидкостей навколо точки з векторною координатою 
.
Така як тепловий рух молекул газу рівновірогідний у всіх напрямках, для визначення відношення 
необхідно просумувати усі елементарні об’єми, що знаходяться на відстані 
і ці об’єми заповнять шаровий прошарок між 2 нескінчено-близькими сферами з радіусами v i v+dv.
Об’єм такого шару:
Ткаим чином, число молекул з швидкостями в інтервалі від v до v+dv буде чисельно дорівнювати:
(11)
- деяка стала, що не залежить від швидкості молекул.
Знайдемо вираз величини А. Так як інтервал швидкостей від нуля до нескінченності охоплює всі молекули, то очевидно, що інтеграл:
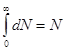
тоді:
Якщо зробити заміну змінних 
і скористатися значенням, що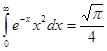 
, то знайдемо:
З урахуванням цього, закон розподілу Максвела:
(12)
Графік функції рівняння (9) представляє собою Гаусову криву розподілу випадкової кривої:
Густина вірогідності розподілу молекул по швидкостям буде мати вигляд:
Як слідує з даного рівняння, при кожній температурі є деяка швидкість, яка має найбільше число молекул (цю швидкість називають найбільш вірогідною). Знайдемо вираз для цієї швидкості з урахуванням рівняння (12), дослідивши дане рівняння на екстремуми. Скоротивши в рівнянні (12) сталі величини і проінтегрувавши, отримаємо:
Звідси знаходимо вірогідну швидкість:
(13)
Середня арифметична швидкість молекул:
Стан газу можна характеризувати однією з трьох швидкостей:
- вірогідною
- середньою арифметичною
- середньою квадратичною
Наприклад:
p,V – тиск і об’єм.
Співвідношення між цими швидкостями:
