Главная | Обратная связь

ВЕРОЯТНОСТЬ СОБЫТИЯ

 

Под событием В понимается всякое происходящее явление. На­пример, попадание в цель при выстреле. Событие называется достовер­ным, если оно должно произойти непременно, и, наоборот, событие на­зывается невозможным, если оно заведомо не наступит.

Допустим, имеется возможность неограниченного повторения ис­пытаний, в каждом из которых при сохранении неизменных условий отмечается появление или непоявление события В. Например, из 10 выстрелов (n) 7 выстрелов (Δn) попали в цель. Отношение принято называть частотой события В, т.е.

 

Р(В) = 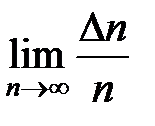= 0,7. (1)

 

Из выражения (1) видно, что вероятность достоверного события Р(В) = 1 при Δn = n, а невозможного Р(В) = 0 при Δn = 0. Таким образом, 0 < Р(В) < 1 при 0 < Δn < n.

 

РАСПРЕДЕЛЕНИЕ СЛУЧАЙНЫХ ОШИБОК ИЗМЕРЕНИЯ.

ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ И ДОВЕРИТЕЛЬНАЯ

ВЕРОЯТНОСТЬ

 

При неоднократном измерении одной и той же величины x ре­зультаты отдельных измерений х_1, х₂...х_n будут неодинаковы из-за наличия случайных ошибок.

В курсе математической статистики доказывается, что наилучшей оценкой истинного значения А измеряемой величины х является ее среднее арифметическое значение:

 

, (2)

 

где n – число измерений; - результат отдельного измерения величины А.

Ошибка нам тоже неизвестна, поэтому имеется какая-то вероятность того, что истинное значение А лежит в некоторых пределах вблизи . Важно найти эти пределы или интервал, в пределах которого с заданной вероятностью обнаружится значение определяемой величины А. Для этого выбирают некоторую вероятность α, близкую к 1, и определяют для нее интервал от до 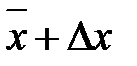, в котором бы находилось значение определяемой величины. Этот интервал называется доверительным интервалом, а вероятность α - доверительной вероятностью, - доверительная граница общей погрешности измерений.

Поясним смысл терминов: доверительная граница общей погрешности и доверительная вероятность α. Для этого используем числовую ось.

Пусть среднее значение измеряемой величины – (рис.1). Отложим 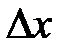от справа и слева. Полученный числовой интервал от до называется доверительным интервалом.

 

 

Рис. 1

 

Результаты ряда измерений можно наглядно представить в виде диаграммы, которая показывает, как часто получаются те или иные значения. Такая диаграмма называется гистограммой.

Чтобы построить гистограмму, надо весь диапазон измеренных значений от x_min до х_max разбить на равные интервалы (рис. 2) и подсчитать относительную частоту Δn/n попаданий результатов измерения в каждый интервал (n – число всех измерений, Δn – число измерений, попадающих в данный интервал).

 

Рис. 2	Рис. 3

 

Если увеличить число измерений, ступенчатая кривая будет приближаться к гладкой кривой, которая называется кривой распределения случайной величины x_i. Величина f(x), пропорциональна доле числа отсчетов Δn/n, попадающей в каждый интервал. Она называется плотностью вероятности.

Смысл плотности вероятности заключается в том, что произведение f(x)dx дает долю полного числа отсчетов n, приходящуюся на интервал от x до x+dx или, иначе говоря, вероятность того, что результат любого отдельного измерения х_i будет иметь значение, лежащее в указанном интервале. Эта вероятность численно равна площади заштрихованной криволинейной трапеции ΔS.

Вся площадь под кривой распределения определяется как произ­ведение вероятности попадания измеренного значения на всю числовую ось х и равна 1, т.е.

 

,

 

где Р(х) – функция распределения случайной величины х.

 

Математически закон распределения случайной величины х выражается законом Гаусса (нормальный закон распределения) и имеет вид

 

f(x)= (3)

 

где f(x) – функция плотности вероятности; е – основание натурального логарифма; х – результат очередного измерения; А – истинное значение измеряемой величины; ² – дисперсия, которая определяется по формуле

 

.

 

Поскольку дисперсия имеет размерность квадрата случайной величины, а это не всегда удобно, то вводится средняя квадратичная ошибка , которая представляет собой положительный квадратный корень из дисперсии:

 

.

 

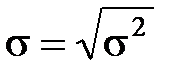Если средняя квадратичная ошибка неизвестна, то вместо нее используют величину S( ) - среднее квадратичное отклонение среднего результата.

 

. (4)

 

Как видно из выражения (3), функция плотности вероятности для распределения Гаусса является функцией двух параметров – А и σ. Распределение Гаусса симметрично относительно А (или ), его ширина пропорциональна σ (рис.4). Чем точнее измерения, тем плотнее вблизи среднего значения лежат результаты отдельных измерений, т.е. величина σ меньше. С уменьшением σ фигура, образуемая кривой распределения, сужается и вытягивается вверх. При этом площади под кривыми распределения будут равны между собой, т.к. вероятность попадания случайной величины на всю числовую ось равна 1. С увеличением числа измерений S( ) стремится к средней квадратичной ошибке

Рис. 4

Следовательно, S( ) является приближенным значением средней квадратичной ошибки σ, т.е. ее оценкой, которая тем ближе к σ, чем больше число измерений. Из формулы (4) следует, что с увеличением числа измерений средняя квадратичная ошибка изменяется обратно пропорционально корню квадратному из числа измерений. Однако в действительности существует предел

уменьшения средней квадратичной ошибки за счет увеличения числа измерений. Существование этого предела обусловлено наличием систематических ошибок, которые в действительности всегда существуют и не изменяются при увеличении числа измерений. Поэтому обычно производят небольшое (5-6) число измерений.

Задаваясь определенной доверительной вероятностью α, можно определить отношение доверительной границы случайной погрешности ε к среднему квадратичному отклонению S( ), т.е. найти

 

 

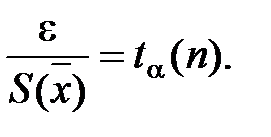
Отношение называется коэффициентом Стьюдента, который не зависит от среднего квадратичного отклонения, а зависит лишь от вы­бора доверительной вероятности и числа измерений n. Это позволило Стьюденту составить таблицу значений коэффициентов (табл. 1).