 |
|
ПРАВИЛЬНОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ
Цель работы: определить плотность твердого тела и на примере ее расчета научиться производить расчет погрешности измерений.
Приборы и принадлежности: тело цилиндрической формы, штангенциркуль.
Теоретические сведения
Плотностью вещества называется физическая величина, равная отношению массы тела m к его объему V:
(1)
Это отношение определяет массу вещества, содержащегося в единице объема.
По формуле (1) можно вычислить плотность только для однородных тел. При неравномерном распределении массы тела по его объему плотность вещества неодинакова в различных частях тела, поэтому вводят понятие плотности в некоторой части тела
,
где dmi - масса вещества в элементарном объеме dVi.
Плотность всего неоднородного тела вычисляют как среднюю плотность вещества
. (2)
В настоящей работе определяют плотность вещества, из которого представлено однородное тело цилиндрической формы. Объем этого тела
. (3)
Подставив (3) в (1), получим формулу для вычисления плотности вещества
, (4)
где масса тела m определяют с помощью технических весов, диаметр D и высоту h измеряют штангенциркулем.
Порядок выполнения работы
1. Записать в таблицу массу тела, указанную на цилиндре.
2. Ознакомиться с измерительным прибором штангенциркулем. Определить точность прибора. Проверить, совпадает ли нуль шкалы штангенциркуля.
3. Измерить на обоих концах цилиндра диаметр с помощью штангенциркуля. Провести 5 измерений, поворачивая цилиндр вокруг его оси. Результаты записать в таблицу.
4. Измерить высоту цилиндра с помощью штангенциркуля 5 раз, повернув перед каждым измерением цилиндр вокруг его оси на некоторый угол (около 45°). Результаты записать в таблицу.
Таблица
| n |  , см
|  , см
|  , см2
| m, г |  , см
|  , см
|  , см2
|
 , см
|  , см
|  , см2
|  , см
|  , см
|  , см2
| ||
5. Вычислить значение границы общей погрешности для массы (Δm), которая определяется только систематической погрешностью по формуле:
,
где δ – предел допускаемой погрешности средства измерения, которую рассчитывают как половина цены наименьшего деления шкалы прибора. Значение коэффициента Стьюдента, соответствующее доверительной вероятности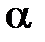 
и числу измерений n находим по таблице коэффициентов Стьюдента (см. стр. 10).
6. Вычислить значение границы общей погрешности для диаметра (ΔD) по формуле:
.
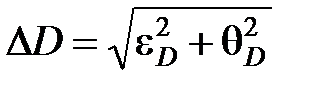Доверительную границу случайной погрешности для диаметра 
рассчитать по формуле:
.
Доверительную границу систематической погрешности для диаметра тела 
рассчитывают по формуле:
.
Значение коэффициентов Стьюдента, соответствующее доверительной вероятности 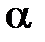и числу измерений n находим по таблице коэффициентов Стьюдента (см. стр. 10).
7. Вычислить значение границы общей погрешности для высоты тела (Δh) по формуле:
.
Доверительную границу случайной погрешности для высоты 
рассчитывают по формуле:
.
Доверительную границу систематической погрешности для высоты тела 
рассчитывают по формуле:
.
8. Вычислить значение доверительной границы общей погрешности для числа p (Δp).
9. Рассчитать значение доверительной границы общей погрешности плотности тела, исходя из формулы:
,
где γ – относительная ошибка
,
– среднее значение плотности тела, определяемое по формуле
.
10. Записать окончательный результат в виде:
г/см3, при 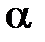= 95%.
Контрольные вопросы
1. Классификация погрешностей.
2. Как рассчитать доверительные границы систематической погрешности прямых однократных измерений, прямых многократных измерений и постоянных величин?
3. Как рассчитать доверительную границу случайной погрешности?
4. При каких условиях можно пренебречь случайной, систематической погрешностями?
5. Как определяются границы общей погрешности прямых измерений?
6. Как рассчитать границу общей погрешности косвенных измерений?
7. Объяснить смысл границы общей погрешности, относительной погрешности и доверительной вероятности?
8. В каком виде записывается окончательный результат проведенных измерений?
ЛАБОРАТОРНАЯ РАБОТА №2