ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩЕНИЯ НА КРЕСТООБРАЗНОМ

МАЯТНИКЕ ОБЕРБЕКА

Цель работы: исследование зависимость момента инерции маятника от расположения грузов, закрепленных на стержне маятника.

Приборы и принадлежности: маятник Обербека, набор грузов и перегрузов, штангенциркуль.

Теоретические сведения

В механике под твердым телом подразумевают абсолютно твердое тело, т. е. тело деформациями которого можно пренебречь. При вращении твердого тела все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Быстроту вращения характеризуют углом поворота тела в единицы времени. Если за любые равные промежутки времени тело поворачивается на одинаковые углы, вращение называется равномерным. Величина, определяющая изменение угла поворота за единицу времени, называется угловой скоростью. Угловая скорость определяется по формуле

Единицей измерения угловой скорости является рад/с. При неравномерном вращении изменение угловой скорости со временем характеризуется угловым ускорением, которое вычисляется по формуле

Единица измерения углового ускорения является рад/с². Угловая скорость ω и угловое ускорение ε связаны с линейной скоростью и линейным (тангенциальным) ускорением следующими соотношениям:

и , (1)

где –расстояние от точек до оси вращения

При вращении тела вокруг неподвижной оси изменение угловой скорости и его движения зависит от действующего момента силы. Моментом силы относительно неподвижной точки О называется векторная величина, определяемая векторным произведением радиуса-вектора , проведенного из точки О в точку Априложения силы, на силу (рис. 1).

где –псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к .


Рис. 1	Рис.2

Модуль момента силы

где –угол между 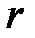и ; 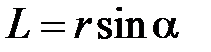–плечо силы - кратчайшее расстояние между линиями действия силы и точкой О.

Моментом силы относительно неподвижной оси ,называется скалярная величина , равная проекции на эту ось вектора момента силы , определенного относительно произвольной точки О, данной на оси 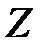(рис. 2). Значение момента не зависит от выбора положения точки О на оси .

Равнопеременное вращательное движение тел характеризуется постоянным угловым ускорением, оно появляется под действием сил, момент которых постоянен по величине и направлению.

Зависимость углового ускорения от момента силы выражена в основном законе динамики вращательного движения

, (2)

где - момент инерции тела.

Момент инерции материальной точки относительно какой-либо оси вращения называется скалярная величина, равная произведению массы m этой точки на квадрат расстояния от точки до оси вращения:

Моментом инерции тела относительно данной оси вращения называют сумму моментов инерции элементарных масс, на которые разбивается тело:

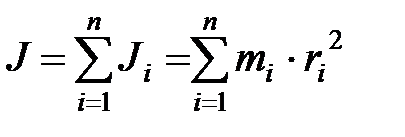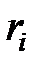где - элементарная масса; - расстояние от элементарной массы до оси вращения.

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела относительно любой оси вращения равен моменту инерции относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния между осями:

Законы вращения тел можно изучить с помощью маятника Обербека.

Рис.3

Рассмотрим движения механической системы представленной на рис. 3. Груз массой m движется с ускорением

под действием результирующей силы тяжести

и силы натяжения нити

(рис. 3). Запишем для груза второй закон Ньютона в проекции на направление движения:

Диск вращается равноускоренно под действием натянутой нити, вызванной силой натяжения нити

. Сила натяжения передается нитью от груза к диску вращающегося маятника.

Если предположить, что нить невесомая, то на диск маятника действует сила , равная по величине и противоположная ей по направлению (следствие третьего закона Ньютона: ). Отсюда

. (3)

Сила натяжения нити создает вращательный момент относительно горизонтальной оси O, направленный вдоль этой оси «от нас» и приводящий в движение маятник Обербека. Величина момента силы равна

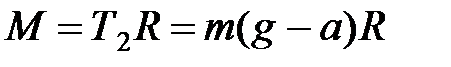, (4)

где 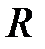– радиус диска, на который намотана нить.

Основной закон динамики вращательного движения (2) в скалярном виде и с учетом момента силы (4) примет вид (записаны проекции векторов моментов сил и углового ускорения на ось вращения О,направление которой выбрано «от нас»):

. (5)

Используя кинематическую связь линейного и углового ускорения (1), а также уравнение движения груза при нулевой начальной скорости , выразим через величины и :

. (6)

Преобразуем уравнение (5), используя выражение (6) и и получим момент инерции маятника Обербека

. (7)

Эту зависимость можно использовать для экспериментальной оценки величины момента инерции маятника Обербека.

Теоретический расчет момента инерции маятника Обербека представляет сумму моментов инерций - момента инерции диска радиусом , - моментов инерции четырех подвижных грузов и - момента инерции крестовины маятника без груза .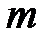

В связи с тем, что размеры грузов малы по сравнению с расстоянием от оси вращения до центров масс грузов, то грузы можно считать материальными точками. Для материальной точки момент инерции равен

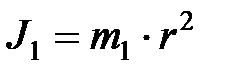где – масса груза на крестовине; – расстояние от оси вращения до центра грузов. Момент инерции крестовины маятника без груза определяется как

где – масса стержня без груза; - длина стержня крестовины.

Таким образом, теоретический расчет момент инерции маятника можно представить следующей формулой

Расчет разности моментов инерции и для двух различных расстояний и позволит исключить слагаемые и 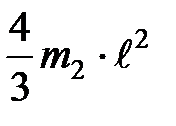. Тогда теоретический расчет момента инерции маятника будет определяться по формуле

. (8)

Расчет момента инерции маятника по формуле (7) при различных расположениях грузов на крестовине можно теоретически проверить величиной момента инерции , рассчитанного по формуле (8).

Описание установки

Для расчетов экспериментального и теоретического моментов инерции представлена установка маятника Обербека (рис. 4, а). Схематический вид установки маятника Обербека показан на рис. 4, б, в.

Маятник Обербека имеет вертикальную колонну 1, которая установлена на основании 2. На вертикальной колонне 1 прикреплены два кронштейна: нижний 3 является неподвижным, верхний 4 - подвижный и две неподвижные втулки: нижняя 5 и верхняя 6. Основание снабжено регулируемыми ножками 7, обеспечивающими горизонтальную установку прибора.

На верхней втулке 6 посредством основания 8 закреплен подшипниковый узел диска 9 и диск 10. Через диск перекидывается нить 11. Один конец нити прикреплен к двухступенчатому диску 12, а на втором конце закреплены грузы 13. На нижней втулке 5 посредством основания 14 прикреплен тормозной электромагнит 15, который удерживает систему крестовины вместе с грузами в состоянии покоя. Подвижный кронштейн 4 можно переместить вдоль колонны и фиксировать его в любом положении, определяя длину пути падающего груза. Для этого на колонне 1 нанесена миллиметровая шкала 16. На подвижном кронштейне 4 укреплен фотоэлектрический датчик 17. На неподвижном кронштейне 3 - фотоэлектрический датчик 18. К кронштейну 3 прикреплен кронштейн 19 с резиновым амортизатором, ограничивающим движение грузов.

Под действием груза нить разматывается и приводит маятник во вращательное движение, которое предполагается равноускоренным. Угловое ускорение при этом тем меньше, чем больше момент инерции системы относительно оси вращения, величина которого зависит от положения перемещаемых грузов на крестовине. Время движения груза измеряется электронным секундомером 18, расположенным у основания прибора, а остановка происходит по сигналу фотодатчика. Груз опускается на расстояние 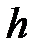, измеряемое вертикально закрепленной линейкой с сантиметровыми делениями.


а	б	в
Рис. 4

Порядок выполнения работы

1. Установить один перегруз на падающий груз. Определить массу общего падающего груза и записать в табл.

2. Измерить с помощью штангенциркуля диаметр диска. Рассчитайте радиус диска и записать в табл..

3. Укрепить на стержне крестовины грузы 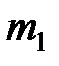на одинаковых расстояниях от оси вращения (в пределах от 5 до 15 см). Определите это расстояние, используя деления нанесенные на стержне (1 деление =1 см) и записать в табл.

4. Вращая маятник рукой, намотать нить на диск и установить падающий груз на высоте (в пределах от 30 до 40 см). Значение высоты записать в таб.

5. Включить электронный секундомер. Нажать кнопку «пуск» и одновременно запустить вращение диска. В момент прохождения грузом нижней точки секундомер остановится. Записать время падения 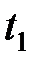груза в табл.

6. Провести прямые пятикратные измерения времени падения груза при неизменной геометрии эксперимента согласно п.п. 4-5. Результаты измерений записать в табл. Рассчитать среднее время падения.

7. Изменить расстояние 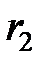от оси вращения до грузов (в пределах от 20 до 25 см) и записать в табл.

8. Провести прямые пятикратные измерения времени падения груза при неизменной геометрии эксперимента согласно п.п. 4-5. Результаты измерений записать в табл. Рассчитать среднее время падения.

Таблица

N	, г	, г	, см	, см	, см	, c	, см	, c





	=	=

9. Вычислить экспериментальные значения моментов инерции маятника и 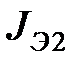с грузами на стержнях, расположенных на разном расстоянии от оси вращения по формуле (7). В качестве времени падения груза взять его среднее значение.

10. Рассчитать теоретическое значение момента инерции маятника для выбранных расстояний по формуле (8).

11. Сравнить полученные результаты и найдите относительную погрешность измерения момента инерции по формуле

где - теоретическое изменение моментов инерции при разных расстояниях; - экспериментальное изменение моментов инерции при разных расстояниях.

Контрольные вопросы

1. Дать определение абсолютно твердого тела и вращательного движения.

2. Дать определение средней и мгновенной угловых скоростей, средней и мгновенной угловых ускорений. Единицы измерения угловой скорости и углового ускорения. Как определяется направления векторов угловой скорости и углового ускорения? Какова связь между линейными и угловыми скоростями и ускорениями?

3. Почему движение падающего груза и вращение маховика являются равноускоренными?

4. Вывести основной закон динамики вращательного движения.

5. Что называется моментом силы тела относительно неподвижной точки вращения? Как определяется его направление? В каких единицах он измеряется?

6. Какая сила сообщает вращающий момент маятнику? Как направлен момент этой силы?

7. Что называется моментом инерции материальной точки и тела? В каких единицах он измеряется? Каков физический смысл момента инерции тела.

8. Сформулируйте и объясните теорему Штейнера.

ЛАБОРАТОРНАЯ РАБОТА №4

⇐ Предыдущая 1 2 3 4 5 678 9 10 Следующая ⇒