Главная | Обратная связь

ОБРАБОТКА РЕЗУЛЬТАТОВ КОСВЕННЫХ ИЗМЕРЕНИЙ

 

При косвенных измерениях физическую величину вычисляют по результатам прямых измерений других величин, с которыми она связана функциональной зависимостью, выражающей физическую закономерность. Например, измерение плотности вещества является косвенным, т.к. ее вычисляют по результатам измерения массы и объёма тела. Пусть искомая физическая величина у связана с другими величинами х_1, х₂, ... х_n некоторой функциональной зависимостью.

 

у = f(х_1, х₂, ... х_n),

 

где х_1, х₂, ... х_n - величины, полученные при прямых измерениях, и табличные данные.

Требуется определить абсолютную Δу и относительную ошибки величины у.

В теории погрешностей доказывается, что абсолютная ошибка (доверительная граница погрешности) косвенного измерения Δу рассчитывается по формуле

 

,

 

где – частная производная функции y = f(x); Δx_i – абсолютная ошибка отдельного прямого измерения.

Абсолютные ошибки Δx₁, Δx₂ определяются для одного и того же значения надежности Р с использованием коэффициентов Стьюдента. Расчет Δx производится по формуле (8). Среднее значение измеряемой величины рассчитывается по формуле (2).

Относительную ошибку косвенных измерений рассчитывают по формуле

. (9)

 

В большинстве случаев проще сначала вычислить относительную ошибку, а затем абсолютную ошибку по формуле

 

. (10)

 

Таким образом, при обработке результатов косвенных измерений:

1. Если искомая физическая величина у представляет собой сумму или разность физических величин, измеряемых непосредственно, то проще сначала найти абсолютную ошибку.

 

. (11)

 

2. Если искомая физическая величина у представляет собой произведение или частное, то легче сначала найти относительную ошибку, которая может быть рассчитана по формуле (9), а затем найти абсолютную по формуле (10).

3. Если в расчетную формулу искомой величины входят величины, которые не измеряют в данном эксперименте и известны с достаточно большой точностью (например, π, g и т.д.), то их значения следует выбирать таким образом, чтобы относительной погрешностью этих величин можно было пренебречь по сравнению с другими погрешностями. Для этого их относительная погрешность должна быть на порядок (в 10 раз) меньше наибольшей относительной погрешности физических величин, измеряемых непосредственно.

Если табличные или экспериментальные данные приводятся без указания погрешности, то абсолютную ошибку принимают равной поло­вине порядка последней значащей цифры. Например: π=3,14, Δπ=0,005.

При обработке результатов измерений необходимо проделать следующее:

1. Провести измерения n раз (обычно 5).

2. Вычислить среднее арифметическое значение по формуле (2).

3. Задать доверительную вероятность α (обычно α = 0,95).

4. По таблице найти коэффициент Стьюдента, соответствующий заданной доверительной вероятности α и числу измерений n.

5. Вычислить случайную и систематическую ошибки по формулам (5), (7) и сравнить их. При дальнейших вычислениях абсолютную ошибку рассчитывают как сумма случайной и систематической, или выбирают большую из них.

6. По формулам (9, 10) вычислить относительную ошибку.

7. Если физическая величина определяется косвенно, то:

а) для формул, где искомая величина представляет сумму или разность физических величин, сначала находится абсолютная ошибка по формуле (11), а затем относительная по формуле (10);

б) для формул, где искомая величина представляет произведение или частное, сначала находится относительная ошибка по формуле (9), а затем абсолютная по формуле (10).

8. Записать окончательный результат в виде

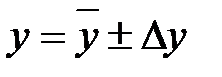, при α = …. .

 

ЛАБОРАТОРНАЯ РАБОТА №1