Главная | Обратная связь

ТРИЗ-задание 31. Поверхностное натяжение твёрдых тел

Наличие силы F₁₃ на рис. 48 говорит о том, что поверхностным натяжением обладают не только жидкости, но и твёрдые тела. Действительно, если на рис. 41 слово «жидкость» заменить на слова «твёрдое тело», то ничего не изменится ни в рисунке, ни в рассуждениях, поскольку и в жидкости, и в твёрдом теле молекулы расположены близко друг к другу. Поверхностное напряжение твёрдого тела в своё время стало причиной брака при производстве полупроводниковых пластин (толщиной 100 мкм и диаметром 40 мм и выше). В.В. Митрофановым было обнаружено следующее явление: кремниевая пластина, стороны которой были обработаны различно – одна сторона полированная, а другая шлифованная (грубо обработанная), изгибается, причем всегда полированная поверхность вогнутая, а шлифованная – выпуклая. Пластинки даже самопроизвольно ломались. Как этого избежать?

Описанный эффект – это эффект Тваймана. Попробуйте сделать несколько изобретений, применив эффект Тваймана для выдвижения идей принципа действия различных измерительных приборов.

В.В. Митрофанов на основе этого и других эффектов сформулировал постулат о диссиметрии (какой?). Диссиметрия – причина любого явления или эффекта и ключ к решению всех загадок природы.

Найдите диссиметрию в явлениях молекулярной физики.

20. МЫЛЬНЫЕ ПУЗЫРИ И Формула Лапласа

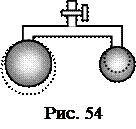Во многих учебниках по физике описывается опыт с двумя мыльными пузырями, соединенными трубкой (рис. 54). В этом опыте маленький пузырь уменьшается, а большой – увеличивается. Почему так происходит? Для объяснения этого выведем формулу для давления под кривой поверхностью жидкости.

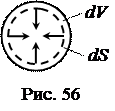
Стремление жидкости к сокращению своей поверхности приводит к тому, что давление под выпуклой поверхностью жидкости оказывается больше, а под вогнутой меньше, чем под плоской (рис. 55). Силы дополнительного давления Dр направлены к центру кривизны поверхности. Вычислим это добавочное давление Dр для пузырька газа, находящегося в жидкости (рис. 56). Пусть под действием давления Dр объём пузырька уменьшился на dV, а поверхность уменьшилась на dS.

Объём шара равен Þ dV = 4pR²dR.

Площадь поверхности равна S = 4pR² Þ dS = 8pR dR.

dA = – Dp dV = – Dp 4pR² dR.

Другая формула для работы: dA = – s dS = – s 8pR dR.

Приравняем уравнения для работ и получим формулу Лапласа для сферической поверхности:

Dp4pR²dR= s8pRdR Þ

В общем случае формула Лапласа имеет вид

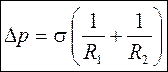, (86)

где R₁ и R₂ – радиусы кривизны двух взаимно перпендикулярных нормальных сечений. В формуле (86) радиус кривизны R считают положительным (рис. 55 б), если центр кривизны находится внутри жидкости (при несмачивании), и радиус кривизны считают отрицательным (рис. 55 в), если центр кривизны лежит над поверхностью (смачиваемость).

Частные случаи формулы Лапласа:

1) для сферы R₁ = R₂ = R и Dp = 2s/R;

2) для плоскости R₁ = R₂ = ¥ и Dр = 0;

3) для цилиндрической поверхности жидкости между двумя параллельными пластинками (рис. 57): R₁ = R, R₂ = ¥ и Dp = s/R;

4) мыльный пузырь имеет две сферические поверхности мыльной плёнки, избыточное давление которых направлено к центру мыльного пузыря, поэтому Dp = 4s/R.

Чем меньше радиус кривизны поверхности жидкости, тем больше давление. Этим и объясняется результат опыта, изображённого на рис. 54. Хотя можно найти и другое объяснение, если подсчитать площади поверхностей двух мыльных пузырей в начале опыта и одного большого пузыря в конце опыта.