 |
|
Идеального газа, при нагревании и плавлении
Расчет изменения энтропии в процессах идеального газа производится по формуле
dS = d (n CV ln T + nR ln V). (70)
Изотермический процесс. Так как T = const, то в формуле (70) первое слагаемое при дифференцировании обратится в нуль: dS = nR d (ln V). Интегрируя, получаем:
 . (71)
. (71)
Из формулы (71) видно, что энтропия возрастает при увеличении объёма газа. Из закона Бойля-Мариотта p1V1 = p2V2 можно произвести замену V2/V1 = p1/p2. Таким образом, получаются формулы
 . (72)
. (72)
Изохорный процесс. Так как V = const, то в формуле (70) второе слагаемое при дифференцировании обратится в нуль: dS = n CV d (ln T). Интегрируя, получаем: DS = n CV ln (T2/T1), т.е. энтропия возрастает при увеличении температуры. Отношение T2/T1 можно заменить отношением p2/p1.
Изменение энтропии можно найти и другим способом, используя молярную теплоёмкость:
 Þ dQ= nCVdT;
Þ dQ= nCVdT;


 . (73)
. (73)
Изобарный процесс (p = const). Для вычисления DS по формуле (70) необходимо выразить температуру Т или объём V из уравнения Менделеева-Клапейрона, например, подставим объём V = nRT/p в формулу (70):

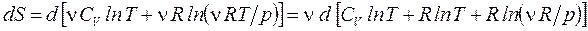 ,
,
|
 ,
,
 .
.
Вычислить DS можно, используя молярную теплоёмкость (кроме того, при р = const возможна замена T2/T1 = V2/V1):
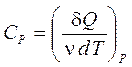 Þ dQ= nCPdT;
Þ dQ= nCPdT;


 . (74)
. (74)
Адиабатический процесс.  , так как DQ = 0 (энтропия не изменяется). При адиабатном расширении газа энтропия возрастает за счет увеличения объёма, но уменьшается за счет понижения температуры, и эти два процесса полностью компенсируют друг друга.
, так как DQ = 0 (энтропия не изменяется). При адиабатном расширении газа энтропия возрастает за счет увеличения объёма, но уменьшается за счет понижения температуры, и эти два процесса полностью компенсируют друг друга.
 Энтропия обладает аддитивностью: энтропия системы равна сумме энтропий тел, входящих в систему. Для нахождения DS в газовых процессах выбираются любые удобные для расчетов процессы.
Энтропия обладает аддитивностью: энтропия системы равна сумме энтропий тел, входящих в систему. Для нахождения DS в газовых процессах выбираются любые удобные для расчетов процессы.
Изменение энтропии при нагревании тел: Q = cm (t2 – t1),
dQ= cmdT;  ;
;  , (75)
, (75)
где с – удельная теплоёмкость.
Изменение энтропии при плавлении.
Q= lm, dQ= ldm,  . (76)
. (76)
Интегрирование ведется от 0 до m, так как идет процесс появления новой фазы вещества. Температура плавления ТПЛ и удельная теплота плавления l – величины постоянные.
Аналогичной формулой выражается изменение энтропии при парообразовании. Только в формулу (76) подставляются температура кипения ТПАР и удельная теплота парообразования r.
Если вещество нагревалось, плавилось, нагревалось, испарялось и т.д., то общее изменение энтропии будет равно сумме изменений энтропии в отдельных процессах:  .
.
Цикл Карно
Теплота и работа как две формы передачи энергии неравноценны. Если механическая работа всегда может самопроизвольно перейти в тепловую энергию, то обратный процесс возможен лишь в тепловых машинах (двигателях).
Круговым процессом, или циклом, называется такая совокупность термодинамических процессов, в результате которых система возвращается в исходное состояние. Все преобразователи энергии (двигатели) работают циклически, т.е. процессы преобразования тепла в работу периодически повторяются.
Тепловой машиной называется периодически действующее устройство, совершающее работу за счет получаемого извне количества теплоты. Тепловая машина состоит из нагревателя, рабочего тела (газ) и холодильника (рис. 30).
Пусть рабочее тело (газ), получив от нагревателя количество теплоты Q1, расширяясь от V1 до V2, совершает работу (поднимает поршень). Для того чтобы вернуться в начальное состояние, надо газ сжать. Чтобы работа за цикл была больше нуля, необходимо сжатие осуществлять при более низком давлении и температуре, т.е. передать часть тепла Q2 холодильнику. Обычно холодильником служит атмосфера.
 |
Поскольку за цикл изменение внутренней энергии равно нулю, то из первого начала термодинамики следует, что работа равна A = Q1 – Q2.
Для характеристики эффективности тепловой машины вводят коэффициент полезного действия (КПД) как отношение совершенной за цикл работы к полученному количеству теплоты:
 . (77)
. (77)
Циклом с максимальным КПД, в котором отсутствуют бесполезные потери тепла, является цикл Карно, состоящий из двух изотерм и двух адиабат. Рассмотрим цикл Карно на диаграмме (p, V), изображенной на рис. 31. Для простоты расчётов возьмём 1 моль газа (из дальнейших расчетов будет видно, что при произвольном числе молей величина n сокращается).
Процесс 1–2. Газ получает от нагревателя (с температурой Т1) количество теплоты Q1 и расширяется. Наилучшим процессом является изотермическое расширение, так как DU = 0 и всё коли- чество теплоты идет на совершение работы:

 .
.
 Процесс 2–3. В точке 2 рабочее тело отключают от нагревателя и заключают в адиабатическую оболочку. Дальнейшее расширение идет в адиабатическом режиме:
Процесс 2–3. В точке 2 рабочее тело отключают от нагревателя и заключают в адиабатическую оболочку. Дальнейшее расширение идет в адиабатическом режиме:
DQ = 0, A2 = -DU = CV (T1 - T2).
Невыгодно просто охладить газ (при постоянном объёме). Газ, адиабатически расширяясь, продолжает совершать работу.
Процесс 3–4. Газ, соединив с холодильником, сжимают изотермически, чтобы не повышать его внутреннюю энергию:
Т2= const, DU= 0,  .
.
Процесс 4–1. Газ сжимают адиабатно, чтобы он нагрелся до температуры нагревателя: DQ = 0, A4 = – DU = CV (T2 – T1).
КПД равен  .
.
Можно показать, что V2/V1 = V3/V4. Для этого запишем уравнения адиабаты для процессов 2–3 и 1–4 и поделим одно уравнение на другое:
 Следовательно,
Следовательно, 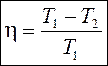 . (78)
. (78)
При выводе формулы КПД не пришлось делать никаких предположений о свойствах рабочего тела и устройстве тепловой машины. Следовательно, мы пришли к теоремам Карно:
1. КПД цикла Карно не зависит от рода рабочего тела и определяется только температурами нагревателя и холодильника.
2. КПД любой необратимой машины (реальной) всегда меньше, чем КПД обратимой машины (Карно), работающей в тех же условиях (Т1, Т2).
Существуют различные формулировки второго начала термодинамики.
Формулировка Кельвина: невозможен вечный двигатель второго рода, т.е. такой периодически действующий двигатель, который бы полностью превращал в работу количество теплоты, взятое от теплового резервуара (т.е. работал бы только за счет охлаждения одного источника теплоты Q1 = A).
Формулировка Клаузиуса: невозможен циклический процесс, единственным результатом которого была бы передача теплоты от менее нагретого тела к более нагретому (т.е. теплота не может самопроизвольно переходить от тела, менее нагретого, к более нагретому).

 Если провести цикл, изображенный на рис. 31, в обратном направлении, то получится цикл холодильной машины. На приведение машины в действие затрачивается работа А (рис. 32). При этом машина отбирает за цикл от тела с температурой Т2 количество теплоты Q2 и отдает телу с более высокой температурой Т1 количество теплоты Q1 = Q2 + A. Эффективность холодильной машины характеризуется её холодильным коэффициентом, который определяется как отношение отнятой от охлаждаемого тела теплоты Q2 к работе А, которая затрачивается на приведение машины в действие:
Если провести цикл, изображенный на рис. 31, в обратном направлении, то получится цикл холодильной машины. На приведение машины в действие затрачивается работа А (рис. 32). При этом машина отбирает за цикл от тела с температурой Т2 количество теплоты Q2 и отдает телу с более высокой температурой Т1 количество теплоты Q1 = Q2 + A. Эффективность холодильной машины характеризуется её холодильным коэффициентом, который определяется как отношение отнятой от охлаждаемого тела теплоты Q2 к работе А, которая затрачивается на приведение машины в действие:

 . (79)
. (79)
Следовательно, без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать её более нагретому (см. формулировку Клаузиуса).
 Подсчитаем КПД цикла Карно для Т1 = 100 °С и Т2 = 0 °С, получим около 27%. Для увеличения КПД обычно увеличивают температуру нагревателя. Примеры КПД: паровоз – 9%, карбюраторный двигатель – 25–30%, дизель – 30–40%, паровая турбина (с температурой пара 500 °С) – 30–40%.
Подсчитаем КПД цикла Карно для Т1 = 100 °С и Т2 = 0 °С, получим около 27%. Для увеличения КПД обычно увеличивают температуру нагревателя. Примеры КПД: паровоз – 9%, карбюраторный двигатель – 25–30%, дизель – 30–40%, паровая турбина (с температурой пара 500 °С) – 30–40%.
 Предельно просто выглядит цикл Карно на диаграмме (T, S). Количества теплоты Q1 и Q2 на рис. 33 – это площади двух прямоугольников (рис. 29):
Предельно просто выглядит цикл Карно на диаграмме (T, S). Количества теплоты Q1 и Q2 на рис. 33 – это площади двух прямоугольников (рис. 29):
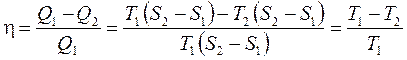 .
.