Главная | Обратная связь

Теоретическое введение.

На всякое тело, двигающееся в вязкой жидкости, действует сила сопротивления. В общем случае величина этой силы зависит от многих факторов: от внутреннего трения жидкости, от формы тела, от характера обтекания и т.д.

Ламинарное (от лат. lamina - слой) течение – течение жидкости, при котором частицы жидкости движутся вдоль прямолинейных траекторий, не перемешиваясь. Такое течение наблюдается при отсутствии внешних воздействий в потоках, движущихся с малыми скоростями.

Когда скорость течения становится значительной, вначале возле стенок трубы, а затем и по всему объему, возникают беспорядочные завихрения жидкости – происходит перемешивание слоев. Такое течение называется турбулентным (от лат. turbulentus - беспорядочный).

Английский ученый О.Рейнольдс в 1883г., исследуя течения жидкостей и газов, обнаружил, что характер их течения зависит от значения безразмерной величины:

,

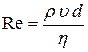называемой числом Рейнольдса. Здесь ρ – плотность жидкости, υ – средняя скорость потока, d – диаметр трубы, η – коэффициент вязкости.

При малых значениях числа Рейнольдса течение является ламинарным, а при больших – турбулентным.

При ламинарном течении жидкость может быть представлена в виде слоев, которые скользят один относительно другого. Такое течение стационарно. При движении слоев жидкости с различными скоростями между ними возникают касательные силы, называемые силами внутреннего трения или силами вязкости.

Внутренние трение(вязкость) – свойство жидкости и газов оказывать сопротивление перемещению одной их части относительно другой. Слой газа или жидкости, движущийся быстрее, ускоряет более медленный слой, который в свою очередь, тормозит более быстрый слой.

Причиной внутреннего трения является наложение упорядоченного движения слоев газа с различными скоростями, и теплового хаотического движения молекул со скоростями, зависящими от температуры. При этом наложении происходит перенос импульсов упорядоченного движения молекул в направлении, перпендикулярном слоям, причем, перенос неравноправный.

Явление внутреннего трения описывается законом Ньютона:

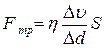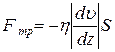, , (1)

где F_тр– сила трения между соседними слоями,

h– коэффициент внутреннего трения или

динамическая вязкость,

Δυ – относительная скорость слоев жидкости,

Δd – расстояние между слоями,

S – площадь соприкосновения слоев,

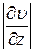– модуль градиента скорости, который

рис.1 характеризует изменение скорости в направлении z, перпендикулярном слоям жидкости (рис.1).

Знак минус в (1) показывает, что сила трения направлена в сторону, противоположную относительной скорости слоя, на который она действует.

Численно коэффициент вязкости h равен силе, действующей на единицу площади слоя при градиенте скорости равном единице.

Единицы измерения h в СИ: .

Динамическая вязкость жидкостей уменьшается с повышением температуры, газов – увеличивается. Это указывает на различия механизма внутреннего трения в этих средах. В жидкостях молекулы распложены близко друг к другу, и вязкость обусловлена межмолекулярным взаимодействием. Эти силы уменьшаются при увеличении температуры, соответственно и вязкость уменьшается. В газах вязкость обусловлена тепловым движением молекул, при увеличении температуры вязкость увеличивается.

Вязкость жидкости также зависит и от давления, но эта зависимость существенно проявляется только при относительно больших изменениях давления (в несколько десятков МПа).

 

В данной работе коэффициент внутреннего трения жидкости определяется методом падающего шарика в жидкости или методом Стокса.

Известно, что в вакууме все тела падают с одинаковым ускорением (g=9,81 м/с²). При падении тела в вязкой покоящейся жидкости на него кроме силы тяжести, действуют выталкивающая сила Архимеда и сила сопротивления (сила внутреннего трения) (рис.2).

Поэтому уравнение динамики для него имеет вид:

F_т – F_A – F = ma (2)

Силу тяжести и выталкивающую силу можно считать постоянными; сила сопротивления F с увеличением скорости возрастает. По мере увеличения скорости наступает такой момент, когда сила тяжести уравновешивается суммой силы Архимеда и силы Стокса. Равнодействующая всех сил становится равной нулю (а = 0):

F_т – F_A – F = 0 (3)

То есть падение шарика в вязкой среде только вначале будет равнопеременным, а через некоторое время шарик будет двигаться практически равномерно.

 

Сила сопротивления при движении шарика – это есть сила внутреннего трения (сила вязкости), значение которой определяется законом Стокса:

F = 6∙p∙h∙r∙υ, (4)

где r – радиус шарика, υ – скорость падения шарика в жидкости, h– коэффициент вязкости жидкости. Эта формула выведена Дж. Стоксом в 1851 г.

рис. 2. Данный закон справедлив для тел сферической формы, при ламинарного обтекания тела жидкостью, лишь для малых чисел Рейнольдса (Re <<1).

 

Сила тяжести равна:

F_т= mg = ρVg, (5)

где т = ρ V – масса шарика, равная произведению объема на плотность материала шарика, g – ускорение свободного падения.

 

Выталкивающая сила Архимеда равна:

F_A = ρ_жgV, (6)

где ρ_ж – плотность жидкости.

 

Подставляем значения сил (4), (5), (6) в уравнение (3), получим:

ρgV – ρ_жgV – 6∙p∙r∙υ∙h = 0 (7)

Решая уравнение движения (7) относительно h, получим для коэффициента внутреннего трения выражение:

6∙p∙r∙υ∙h = ρgV – ρ_жgV 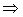(8)

Учитывая, что объем шарика равен:

, (9)

Скорость при равномерном движении определяется выражением:

, (10)

где ℓ - расстояние между метками на цилиндре.

Подставляем (9), (10) в (8), получим выражение для коэффициента внутреннего трения:

(11)

 

Измеряя на опыте d, t, ℓ , зная плотность материала шарика r и плотность исследуемой жидкости r_ж, из (11) можно определить коэффициент внутреннего трения жидкости.

 

Описание прибора.

Для измерения используется стеклянный цилиндр, наполненный исследуемой жидкостью (глицерин). Диаметр сосуда ~ 4-5 см, высота ~ 60-70 см. На цилиндре нанесены две горизонтальные метки m и n, расположенные друг от друга на некотором расстоянии ℓ (рис. 2).

Верхняя метка (метка m) располагается ниже уровня жидкости исоответствует той высоте, на которой силы, действующие на шарик, уравновешивают друг друга, и движение становится равномерным, то есть скорость устанавливается.