Главная | Обратная связь

Теоретическое введение.

 

Во всех реальных жидкостях при их течении, то есть при перемещении одних слоев жидкости относительно других, возникают силы внутреннего трения. Молекулы слоя, двигающегося более быстро, переходят в слой, двигающийся медленнее, и передают при этом некоторое количество движения. Молекулы же слоя, двигающегося медленнее, при переходе в более быстрый слой тормозят его движение, уменьшая среднее количество движения молекул. Такое течение стационарно. При движении слоев жидкости с различными скоростями между ними возникают касательные силы, называемые силами внутреннего трения или силами вязкости.

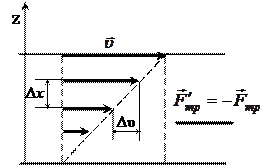В случае установившегося слоистого течения вязкой жидкости, так называемого ламинарного или безвихревого течения, сила внутреннего трения Fв соответствии с законом Ньютона равна:

 

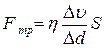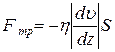, , (1)

рис.1 где F_тр– сила трения между соседними слоями,

h– коэффициент внутреннего трения или динамическая вязкость,

Δυ – относительная скорость слоев жидкости,

Δd – расстояние между слоями, S – площадь соприкосновения слоев,

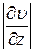– модуль градиента скорости, который характеризует изменение скорости в направлении z, перпендикулярном слоям жидкости (рис.1).

 

 

Численно динамическая вязкость h равна силе, действующей на единицу площади слоя при градиенте скорости равном единице.

Единицы измерения h в СИ: .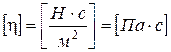

При практических и теоретических расчетах часто приходится встречаться с понятием кинематической вязкостьюν, равной отношению динамической вязкости h к плотности жидкости ρ при той же температуре:

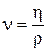(2)

Данное название величины обусловлено тем, что в размерность ν входят только кинематические величины.

Если рассматривать данное явление с точки зрения МКТ, то внутреннее трение – результат переноса импульса от одного слоя к другому, который осуществляется молекулами в процессе их теплового движения.

Вязкость жидкостей и газов зависит от температуры. С повышением температуры вязкость газов увеличивается, а вязкость жидкостей уменьшается. В первом приближении для жидкостей эта зависимость починяется закону:

, (3)

где k – коэффициент пропорциональности, связанный с природой жидкости и ее химическим составом.

Рассмотрим движение жидкости по трубке круглого сечения. При малых скоростях потока движение оказывается ламинарным (от лат. lamina - слой).

При таком течении отдельные слои жидкости движутся с различными скоростями, не перемешиваясь. Скорости частиц медленно меняются от точки к точке и направлены вдоль оси трубки.

С увеличением скорости, вначале возле стенок трубы, а затем и по всему объему возникают завихрения

рис.2 жидкости, слои перемешиваются. Такое течение называется турбулентным (от лат. turbulentus - беспорядочный). Скорость в каждой точке при таком течении быстро меняет величину и направление, сохраняется только средняя величина скорости.

Характер течения жидкости в трубке определяется безразмерной величиной – числом Рейнольдса (Re):

,

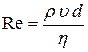где ρ – плотность жидкости, υ – средняя скорость потока, d – диаметр трубы,

η – коэффициент вязкости.

При малых значениях числа Рейнольдса (Re≤1000) наблюдается ламинарное течение, переход от ламинарного к турбулентному происходит в области 1000≤Re≤2000, а при Re = 2300 (для гладких труб) течение турбулентное.

При ламинарном течении у стенок прямолинейной трубы скорость равна нулю, а в центре трубы на оси она максимальна (рис.2). С расстоянием r от оси трубы эта скорость изменяется по параболическому закону:

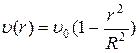(4)

где R – радиус трубы, υ₀ – скорость жидкости на оси трубы.

Данная скорость равна:

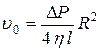, (5)

где ΔP = (P₁ – P₂) – разность давлений на концах трубы, l – длина трубы,

η – динамическая вязкость жидкости.

На преодоление сил внутреннего трения в потоке постоянно затрачивается некоторая энергия. В частности, это подтверждает уменьшение давления в потоке жидкости по горизонтальной трубе одинакового сечения. В случае идеальной невязкой жидкости давление было бы постоянно, то есть Р₁ = Р₂.

Исследуя поток жидкости в капиллярных трубках, в которых сохраняется стационарный поток (устраняются перемешивание и вихревое движение), французский ученый Ж.Л.М. Пуазейль (1799-1869) установил, что уменьшение давления ΔP в потоке зависит от радиуса трубки R, коэффициента вязкости жидкости η, длины трубки l и скорости потока υ:

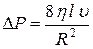(6)

Определив скорость из этого выражения, подставив это значение в формулу для вычисления объема жидкости 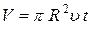, вытекающей через капилляр за время t, то получим, что объем жидкости, протекающий через узкий канал известного радиуса (R) и длины (l), равен:

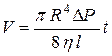, (7)

В таком виде формулу Пуазейля применяют для экспериментального определения коэффициента вязкости жидкости.

Условия, при которых справедлива формула (7): с достаточным запасом должно выполняться неравенство Re < 1000, при течении сквозь трубку не должно происходить существенное изменение удельного объема (для жидкости это условие выполняется практически всегда).

Если жидкость вытекает под действием собственного веса (при вертикальном расположении трубки), то разность давлений равна гидростатическому давлению, т.е. DP = (P₁ – P₂) = ρ g h, (8)

 

где ρ – плотность жидкости, h – высота столба жидкости,

g – ускорение свободного падения.

 

 

В этом случае:

(9)

Вязкость – важнейшая характеристика жидкостей и газов. Вследствие вязкости вода или воздух создают значительное сопротивление быстроходному транспорту; в трубопроводах вязкость жидкостей и газов обуславливает спад давления; вязкость характеризует качество технических масел и т.д.