Главная | Обратная связь

Краткие теоретические сведения

Тела, состоящие из огромного числа молекул и атомов, называют макроскопическими. Объяснить свойства макроскопических тел, опираясь на законы, которым подчиняются микроскопические частицы, позволяет специальный статистический метод, базирующийся на теории вероятностей.

Если частицы подчиняются законам классической механики, то для описания поведения изолированной системы частиц используют классическую статистическую физику, основанную на следующих общих положениях:

а) в системе выполняются законы сохранения импульса, момента импульса, энергии, электрического заряда и числа частиц;

б) все макроскопические параметры системы могут принимать любые значения (спектр значений физических величин непрерывен);

в) все частицы различимы между собой;

г) значения координат и импульсов любых двух частиц независимы.

Абстрактное многомерное пространство, координатами которого служат обобщенные координаты и импульсы системы, называется фазовым прост-ранством. Так как состояние каждой частицы макроскопического тела определяется тройкой координат x, у, z и тройкой соответствующих проекций импульса p_x, p_у, p_z, то состояние системы из N частиц определяется заданием 6N переменных. Число «взаимно перпендикулярных» координатных осей соот-ветствующего фазового пространства равно 6N.

Функцию распределения по импульсам и координатам частиц равновесного классического идеального газа, находящегося во внешнем потенциальном поле, называют распределением Максвелла – Больцмана и записывают в виде:

(1)

где – кинетическая энергия частицы с импульсом р и массой m₀;

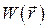– потенциальная энергия этой же частицы;

k_Б– постоянная Больцмана; постоянная А в формуле определяется условием нормировки.

Функцию распределения

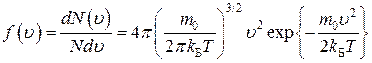(2)

по скоростям теплового движения молекул газа, находящегося в состоянии термодинамического равновесия в отсутствие внешних потенциальных полей, называют распределением Максвелла. Физический смысл этой функции в том, что она показывает относительное число молекул 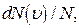модуль скорости которых заключен в интервале от до .

С помощью функции распределения Максвелла можно найти среднее значение любой функции, зависящей от скорости частицы, например:

среднее значение модуля скорости:

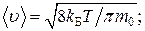(3)

средняя квадратичная скорость:

(4)

наиболее вероятная скорость:

(5)

Конкретная форма графика функции распределения Максвелла (например, высота и ширина пика) зависит от рода газа (массы молекул) и от температуры. Графики распределения f(u) для двух различных значенийтемпературы газа представлены на рис. 1.

Из рис. 1 видно, что функция распределения f(u) стремится к нулю при u ® 0 и u ® ¥. Следовательно, относительное число молекул в газе, обладающих очень малыми и очень большими скоростями, ничтожно мало.

Если идеальный газ находится во внешнем потенциальном поле, например, в гравитационном, то найти концентрацию частиц в элементе объема позволяет распределение Больцмана:

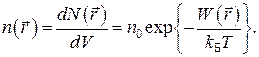(6)

Распределение концентрации молекул идеального газа в однородном поле тяжести при постоянной для всех значений высоты температуре можно определить по барометрической формуле:

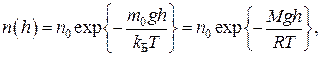(7)

где g – ускорение свободного падения вблизи поверхности планеты;

h – высота над поверхностью планеты;

n₀ – концентрация молекул на поверхности (h = 0);

– потенциальная энергия частицы на высоте h;

R – универсальная газовая постоянная;

M – молярная масса газа.