 |
|
Краткие теоретические сведения
Если частицы подчиняются законам квантовой механики, то для описания поведения изолированной системы частиц используют квантовую статис-тическую физику, основанную на следующих общих положениях:
а) в системе выполняются законы сохранения импульса, момента импульса, энергии, электрического заряда и числа частиц;
б) спектр значений физических величин может быть дискретным, непрерывным и смешанным; энергетический спектр систем, занимающих ограниченную область пространства, дискретен;
в) все частицы одного сорта (тождественные частицы) неразличимы между собой;
г) состояние микрочастицы описывается волновой функцией, позволяющей вычислять лишь вероятность (|ψ|2) нахождения микрочастицы в окрестнос-тях той или иной точки пространства.
Квантовая механика накладывает ограничение на объем элементарной ячейки фазового пространства (фазовый объем): он не может быть меньше, чем h3 (h – постоянная Планка).
Фундаментальный принцип неразличимости тождественных частиц допускает существование двух типов симметрии волновой функции квантовых систем тождественных частиц. Если при перестановке частиц волновая функция не меняет знак:
ψ(х1, х2) = + ψ(х2, х1), (8)
то она называется симметричной, если меняет:
ψ(х1, х2) = – ψ(х2, х1), – (9)
антисимметричной. В выражениях (8) и (9) х1 и х2 – соответственно совокупность пространственных и спиновых координат первой и второй частиц.
В зависимости от характера симметрии волновой функции все элементарные частицы делятся на два класса: фермионы и бозоны.
Описываемые антисимметричными волновыми функциями фермионы (например, электроны, протоны, нейтроны) имеют полуцелый спин и подчиняются статистике Ферми – Дирака. Для них выполняется принцип Паули: в сис-теме тождественных фермионов любые два из них не могут одновременно находиться в одном и том же состоянии. В соответствии с принципом Паули в каждой элементарной ячейке фазового пространства системы тождественных фермионов не может находиться более двух частиц.
Описываемые симметричными волновыми функциями бозоны имеют целый спин (например, π-мезоны, фотоны, фононы) и подчиняются статистике Бозе – Эйнштейна.
Если энергетическому уровню соответствует несколько различных состо-яний квантовой системы, то он называется вырожденным. Если энергетическому уровню соответствует только одно состояние, то он называется невырожденным. Число различных квантовых состояний, характеризующихся одним и тем же значением энергии, т.е. кратность вырождения уровня, называют статис-тическим весом 
. Идеальный газ называется невырожденным, если число возможных состояний (статистический вес) при данной температуре много больше числа частиц газа: 
. Такой газ подчиняется классической статис-тике. Идеальный газ называется вырожденным, если 
Такой газ подчиняется квантовой статистике. Системы невзаимодействующих тождественных бозонов или фермионов называются квантовым идеальным бозе- или ферми-газом. Состояние бозе- или ферми-газа задается с помощью чисел заполнения ni, указывающих количество частиц, находящихся в i-м квантовом состоянии, характеризуемом определенным набором квантовых чисел. Для системы бозонов числа заполнения могут принимать любые целые значения: 0, 1, 2, …,. Для системы фермионов из-за принципа Паули числа заполнения могут принимать лишь два значения: 0 – для свободных состояний и 1 – для занятых. Сумма всех чисел заполнения должна быть равна числу частиц системы. Квантовая статис-тика позволяет рассчитать среднее число частиц (среднее число заполнения <ni>) в каждом квантовом состоянии.
Распределение Ферми – Дирака фермионов идеального ферми-газа по энергиям имеет вид:
(10)
Распределение Бозе – Эйнштейна бозонов идеального бозе-газа по энергиям имеет вид:
(11)
Параметр распределения μ называется химическим потенциалом, не зависит от энергии, а определяется только температурой и плотностью числа частиц. Химический потенциал μ при большом числе частиц в системе можно понимать как минимальное приращение внутренней энергии теплоизолированной системы с неизменным объемом при добавлении одной частицы.
При малых (по сравнению с единицей) числах заполнения распределения Ферми – Дирака (10) и Бозе – Эйнштейна (11) переходят в классическое распределение Максвелла – Больцмана (1):
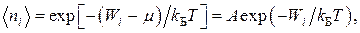(12)
где А = ехр(μ/kБТ).
Температурой вырождения называют температуру, ниже которой отчетливо проявляются квантовые свойства идеального газа. Вырождение газа становится существенным при низкой температуре и большой плотности. Если температура выше температуры вырождения, то поведение газа описывается классическими законами.
Излучение, находящееся в равновесии со стенками полости, в которой оно заключено, можно представить как идеальный фотонный газ. Фотоны являются бозонами, так как спин фотона равен единице. Стенки полости непрерывно излучают и поглощают фотоны, поэтому число фотонов меняется (в зависимости от объема и температуры полости), их распределение по состояниям описывается формулой:
(13)
Энергия фотона Wi = ћωi не зависит от координат и направления его движения, а определяется только модулем ее импульса: W = f(p). Объемная плотность энергии электромагнитного излучения, приходящейся на единичный интервал частот, определяется законом излучения Планка:
(14)