 |
|
Задания для самостоятельного решения
1)Фазовым пространствомназывают 1) абстрактное пространство, координатами которого служат все обобщенные координаты и импульсы системы; 2) абстрактное пространство всех возможных фаз косинусов или синусов; 3) конкретное пространство, заполненное идеальным газом, находящимся в какой-либо одной фазе; 4) пространство всех возможных фаз (в частности, агрегатных состояний) конкретного вещества.
2)Пусть классическая макроскопическая система имеет K степеней свободы. Тогда фазовое пространство системы является 1) K-мерным; 2) (K - 1)-мерным; 3) (2K - 1)-мерным; 4) 2K-мерным.
3)В статистической физике энтропия – мера 1) беспорядка системы; 2) внутренней энергии системы; 3) действия силы на систему; 4) количества теплоты, полученного системой.
4)Энтропия в системе СИ 1) измеряется в К; 2) измеряется в эрг; 3) измеряется; в Дж/К; 4) является безразмерной величиной.
5)При возрастании статистического веса вероятность реализации макросостояния 1) возрастает; 2) не меняется; 3) убывает; 4) ведет себя по-разному в зависимости от других факторов.
6)При возрастании статистического веса энтропия макросостояния 1) возрастает; 2) не меняется; 3) убывает; 4) ведет себя по-разному в зависимости от других факторов.
7)При возрастании статистического веса внутренняя энергия макросос-тояния 1) возрастает; 2) не меняется; 3) убывает; 4) ведет себя по-разному в зависимости от других факторов.
8) Необратимые процессы, происходящие с увеличением энтропии, соответствуют эволюции системы 1) к более вероятным состояниям; 2) к менее вероятным состояниям; 3) к состояниям, имеющим ту же вероятность; 4) к состо-яниям как с большей или меньшей так и с той же вероятностью.
9) Необратимые процессы, происходящие с уменьшением энтропии, соответствуют эволюции системы 1) к более вероятным состояниям; 2) к менее вероятным состояниям; 3) к состояниям, имеющим ту же вероятность; 4) к состояниям как с большей или меньшей, так и с той же вероятностью.
10) Обратимые процессы соответствуют эволюции системы 1) к более вероятным состояниям; 2) к менее вероятным состояниям; 3) к состояниям, имеющим ту же вероятность; 4) к состояниям как с большей или меньшей, так и с той же вероятностью.
11)Функция распределения системы в статистической физике позволяет вычислить 1) вероятности различных значений любой физической величины, зависящей от состояния системы; 2) точное значение любой физической величины, зависящей от состояния системы, в любой момент времени; 3) зависимость от времени вероятности различных значений любой физической величины, зависящей от состояния системы; 4) зависимость от температуры вероятности различных значений любой физической величины, зависящей от состояния системы.
12)Функция распределения системы в статистической физике позволяет вычислить 1) зависимость от температуры вероятности различных значений любой физической величины, зависящей от состояния системы; 2) среднее значение любой физической величины, зависящей от состояния системы; 3) точное значение любой физической величины, зависящей от состояния системы, в любой момент времени; 4) зависимость от времени вероятности различных значений любой физической величины, зависящей от состояния системы.
13)Самое общее распределение, позволяющее определять статистические (термодинамические) свойства систем с переменным числом частиц, называется распределением 1) Бозе – Эйнштейна; 2) Больцмана; 3) Гиббса; 4) Максвелла.
14) Распределение классических нерелятивистских частиц физической системы, находящейся в статистическом равновесии, по модулю или по проекциям скорости называется распределением 1) Больцмана; 2) Гиббса; 3) Максвелла; 4) Ферми – Дирака.
15) Распределение классических нерелятивистских частиц физической системы, находящейся в статистическом равновесии, по координатам называется распределением 1) Больцмана; 2) Гиббса; 3) Максвелла; 4) Ферми – Дирака.
 16) Укажите на оси абсцисс графика функции распределения молекул идеального газа по модулям скорости (рис. 2) точку, соответствующую наиболее вероятной скорости. 1) 1; 2) 3; 3) 4; 4) 2.
16) Укажите на оси абсцисс графика функции распределения молекул идеального газа по модулям скорости (рис. 2) точку, соответствующую наиболее вероятной скорости. 1) 1; 2) 3; 3) 4; 4) 2.
17) На рис. 3 приведен график функции распределения молекул по скоростям (распределения Максвелла). Что выражает площадь заштрихованной полоски? 1) Относительное число молекул, модуль скорости которых лежит в интервале от u до u + du; 2) число молекул, модуль скорости которых равен u; 3) наиболее вероятную скорость; 4) число молекул, модули скорости которых лежат в интервале от u до u + du.
18) Полная площадь под кривой функции распределения Максвелла молекул газа по ско-ростям 1) зависит от температуры газа; 2) зависит от рода газа; 3) зависит от числа молекул газа; 4)не зависит от факторов, перечисленных в вариантах 1 – 3.
19) Чему равно отношение средней квадратичной скорости молекул газа к наиболее вероятной скорости? 1)  ; 2)
; 2) 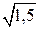 ; 3)
; 3)  ; 4)
; 4)  .
.
20)Как изменится площадь под кривой распределения Максвелла молекул по скоростям при увеличении температуры газа? 1) Увеличится; 2) уменьшится; 3) не изменится.
21)При увеличении температуры газа максимум кривой распределения Максвелла молекул по скоростям 1) сместится в сторону более низких скоростей; 2) сместится в сторону более высоких скоростей; 3) не сместится.
22)Кривая распределения Максвелла молекул по скоростям при увеличении температуры газа 1) станет более пологой; 2) станет более «острой»; 3) не изменится.
23)Какая физическая величина обозначена символом  в формуле распределения Больцмана
в формуле распределения Больцмана  ? 1) Внутренняя энергия всех молекул газа; 2) потенциальная энергия молекул, положение которых определяется радиусом-вектором
? 1) Внутренняя энергия всех молекул газа; 2) потенциальная энергия молекул, положение которых определяется радиусом-вектором  ; 3) кинетическая энергия молекул, положение которых определяется радиусом-вектором
; 3) кинетическая энергия молекул, положение которых определяется радиусом-вектором  ; 4) полная механическая энергия всех молекул.
; 4) полная механическая энергия всех молекул.
24) Если считать температуру идеального газа одинаковой на всех высотах, то распределение концентрации частиц идеального газа вблизи поверхнос-ти планеты определяется 1) барометрической формулой; 2) уравнением состояния идеального газа; 3) распределением Максвелла; 4) уравнением изотерми-ческого процесса.
25)Почему молекулы воздуха в атмосфере Земли не собираются на ее поверхности? 1) Сила тяготения компенсируется выталкивающей силой; 2) сила тяготения много меньше выталкивающей силы; 3) сила тяготения компенсируется силами теплового взаимодействия молекул; 4) сила тяготения компенсируется силами отталкивания молекул при взаимодействии.
26)Барометрическая формула показывает 1) зависимость атмосферного давления от высоты; 2) зависимость концентрации молекул газа от их энергии; 3) увеличение концентрации молекул с увеличением высоты; 4) уменьшение атмосферного давления с уменьшением высоты.
27)Барометрическая формула получена для случая 1) уменьшения температуры атмосферы с увеличением высоты и одинакового модуля ускорения модуля свободного падения; 2) одинаковой температуры атмосферы на любой высоте и уменьшения модуля ускорения свободного падения с увеличением высоты; 3) одинаковой температуры атмосферы на любой высоте и одинакового модуля ускорения свободного падения на любой высоте; 4) уменьшения температуры атмосферы с увеличением высоты и уменьшения модуля ускорения свободного падения с увеличением высоты.
28)Как отличаются значения атмосферного давления при одной и той же температуре воздуха на высотах, одна из которых втрое больше другой? 1)  ; 2)
; 2) 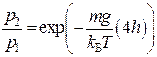 ; 3)
; 3) 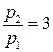 ; 4)
; 4) 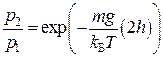 .
.
29) При температуре 20 °C давление воздуха у поверхности Земли в 1,02 раза больше давления воздуха на высоте 1) 0,1 м; 2) 1,8 м; 3) 117 м; 4) 1713 м.
3. КВАНТОВЫЕ СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ