 |
|
КРИТЕРИИ ДОСТОВЕРНОСТИ
| Средние величины | Относительные величины |
| 1. Ошибка репрезентативности | |
m =  где σ – среднее квадратичное
отклонение
n – число наблюдений
где σ – среднее квадратичное
отклонение
n – число наблюдений
| m =  где P – относительная величина, выраженная в %;
q – 100 P;
n – число наблюдений.
где P – относительная величина, выраженная в %;
q – 100 P;
n – число наблюдений.
|
| 2.Доверительная граница – граница, в которых будет находиться значение средней или относительной величины в генеральной совокупность. | |
Mген. = Мвыб.  tm
где Мген. - значение средней величины в генеральной совокупности;
Мвыб.- значение средней величины, полученное в результате исследований на выборочной совокупности; tm
где Мген. - значение средней величины в генеральной совокупности;
Мвыб.- значение средней величины, полученное в результате исследований на выборочной совокупности;
| Рген. = Рвыб.  tm
где Рген. - значение относительной величины в генеральной совокупности;
Рвыб.- значение относительной величины, полученное в результате исследований на выборочной совокупности; tm
где Рген. - значение относительной величины в генеральной совокупности;
Рвыб.- значение относительной величины, полученное в результате исследований на выборочной совокупности;
|
| m - ошибка репрезентативности;, t доверительный коэффициент, устанавливаемый самим исследователем в зависимости от заданной вероятности безошибочного прогноза | |
| 3. Оценка достоверности различий двух средних или относительных величин по t-критерию. | |
t =  где
где  и и  - сравниваемые
средние величины; - сравниваемые
средние величины;
| t =  где
где 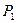 и и  - сравниваемые
средние величины; - сравниваемые
средние величины;
|
| m1 и m2 - ошибка репрезентативности; Различия достоверны при t≥2, что соответствует вероятности безошибочного прогноза, равной 95% и более (Р > 95%). |
Задача-эталон N4
Определение средней ошибки средней арифметической и доверительных границ средней величины. Используем среднюю арифметическую, полученную при решении задачи-эталона N1 и среднее квадратическое отклонение, рассчитанное в задаче-эталоне N3. Необходимо определить ошибку репрезентативности и доверительные границы средней величины. Средняя длительность лечения 37 больных ангиной составила 10.8 дней).
| М = 108.8 | σ = 2.7 | n = 37 |
а) для расчета ошибки репрезентативности используем формулу:
m =  =
=  =
=  =
=  0.4 дня.
0.4 дня.
в) доверительные границы вычисляем по формуле:
Mген. = Мвыб.  tm
tm
при Р = 95%, t = 2,
Мген. = 10.8  2×0.4 = 10.8
2×0.4 = 10.8  0.8 = 10 ÷ 11.6 (дней)
0.8 = 10 ÷ 11.6 (дней)
Следовательно, с вероятностью безошибочного прогноза, равной 95% можно утверждать, что в генеральной совокупности средняя длительность лечения больных ангиной будет находиться в пределах от 10 до 11.6 дней,
при Р = 99%, t = 3,
Мген. = 10.8  3×0.4 = 10.8
3×0.4 = 10.8  1.2 = 9.6 ÷ 12 (дней)
1.2 = 9.6 ÷ 12 (дней)
Следовательно, с вероятностью безошибочного прогноза равной 99% можно утверждать, что в генеральной совокупности средняя длительность леченая больных ангиной будет находиться в пределах от 9.6 до 12 дней.
Задача-эталон N5.