Главная | Обратная связь

УЧЕБНЫЙ МОДУЛЬ 1.3. ЛАБОРАТОРНЫЙ ПРАКТИКУМ

Лабораторная работа № 10

ИССЛЕДОВАНИЕ СВОЙСТВ ПАССИВНЫХ

ЧЕТЫРЕХПОЛЮСНИКОВ

При подготовке к выполнению лабораторной работы необходимо изучить: стр. 108-120 (1) или 404-424 (2) или 213-224, 443-450 (3).

ЦЕЛЬ РАБОТЫ: экспериментальное определение первичных и вторичных (характеристических) параметров четырехполюсника. Исследование режима роботы проходного четырехполюсника при согласованной и несогласованной нагрузке.

КРАТКИЕ ПОЯСНЕНИЯ

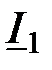
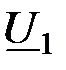
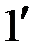
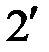
Электротехническое устройство с двумя парами зажимов, при помощи которых оно соединяется с другими участками электрической цепи, назы­вается четырехполюсником. Условное изображение пассивного линейного четырехполюсника, включенного между источником с ЭДС Е и сопротив­лением нагрузки Z_H , показано на рис.10.1. Зажимы 1-1' называются пер­вичными (входными), а зажимы 2-2'-вторичными (выходными) зажимами четырехполюсника. Параметры элементов и схема их соединения внутри четырехполюсника предполагаются неизменными.

1¢

 

 

 

Рис.10.1

Тогда на фиксированной частоте напряжение и ток на первичных зажимах определяются через напряжение и ток на вторичных зажимах системой двух уравнений типа [A]:

где коэффициенты А, В, С и D являются комплексными постоянными, причем А и D - безразмерны, В имеет размерность сопротивления, а С - проводимости. Кроме системы с уравнениями (1) и (2) можно записать еще пять систем уравнений.

Отметим, что уравнения (1) и (2) дают связь входных величин через вы­ходные, т.е. описывают режим прямого питания. При обратном питании (источник подключается к вторичным зажимам, а нагрузка - к первичным) входные величины U₂ и I₂ будут выражаться через выходные величины U₁ и I₁ уравнениями:

Сопоставляя (3) и (4) с (1) и (2), видим, что при обратном питании ко­эффициенты А и D поменялись местами.

Входное сопротивление четырехполюсника со стороны первичных за­жимов (при прямом питании) удобно записать в таком виде:

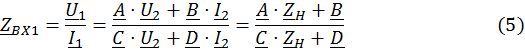
Тогда входное сопротивление четырехполюсника со стороны вторичных зажимов (при обратном питании) будет

Если осуществить режимы холостого хода (Z_H =∞) и короткого замыка­ния (Z_H=0), то соответственно из (5) и (6) получим

Из полученных соотношений видно, что

а это значит, что из четырех полученных входных сопротивлений только три являются независимыми.

Учитывая, что для взаимного четырехполюсника:

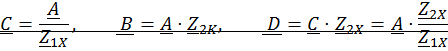
можно получить

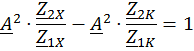
Отсюда

Таким образом, для взаимного четырехполюсника достаточно измерить три входных сопротивления, например , Z_1X , Z_2X , Z_2K , по (8) вычислить коэффициент А, затем определить

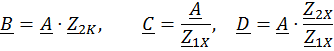
При этом следует учесть, что из (8) получаем два комплексных значения А, отличающихся аргументом на 180° . Для того чтобы правильно выбрать аргумент комплекса А, необходимо, как это следует из (1), измерить U_lx и U_2X в режиме холостого хода на вторичных зажимах и А вычислить из соотношения

Схема для измерения U_2X при заданном значении U₁ представлена на рис.10.2. По этой схеме

где – угол, отсчитанный по шкале фазометра.

Рис. 10.2.

Несимметричный пассивный четырехполюсник, кроме первичных параметров А, В, С и Dили Z_1X, Z_1K, Z_2X, Z_2K, характеризуется передаточной функцией по напряжению:

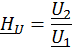
и по току:

по сопротивлению:

или проводимости:

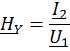
при произвольной нагрузке. Передаточные функции четырехполюсника можно выразить через его - параметры.

Например,

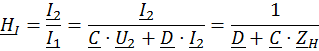
(9)

[A]-параметры четырехполюсника можно определить из опытов холостого хода (ХХ) и короткого замыкания (КЗ):

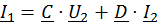(10)

1.Опыт ХХ: 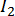=0:

(11)

2. Опыт КЗ: U₂=0:

[A]-параметры можно рассчитать через входные сопротивления четырехполюсника в предельных режимах, т.е. в режимах ХХ и КЗ. Для симметричного четырехполюсника выполняются соотношения:

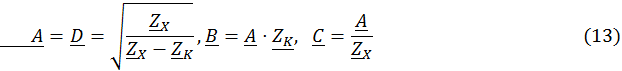
Если известны [A]-параметры четырехполюсника, то параметры [Z], [Y], [H], [G] можно рассчитать, воспользовавшись справочными таблицами (смотри приложение П-1)Б устанавливающими связь между различными системами параметров.

Входные сопротивления четырехполюсника при прямом Z_ВХ1 и обрат­ном Z_ВХ2 включении равны:

 

(14)

Известно, что генератор с внутренним сопротивлением Z_Г – отдает мак­симальную полную мощность в нагрузку Z_H , согласованную с его внут­ренним сопротивлением Z_H = Z_Г. Для согласования генератора и нагруз­ки с разными сопротивлениями между генератором и нагрузкой включают пассивный четырехполюсник, как это показано на рис.10.3.

 

Рис. 10.3.

Входные сопротивления четырехполюсника в этом режиме обозначают­ся Z_С1 и Z_С2 и называются характеристические сопротивления. Условия согласования четырехполюсника записывают так:

со стороны входа: Z_Г=Z^*_C1

cо стороны нагрузки: Z_H=Z_C

Характеристические сопротивления можно определить через [А]- параметры или через входные сопротивления в режиме холостого хода и короткого замыкания.

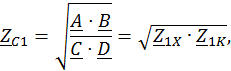
Постоянная передачи g = а + jb рассчитывается при согласованном ре­жиме работы четырехполюсника по формуле:

 

(16)

 

Или через [A]-параметры:

(16a)

где:

a – коэффициент затухания, Нп или дБ;

b – коэффициент фазы, рад.

1 Нп = 8,68 дБ; 1дБ = 0,115 Нп; 1 рад = 57,3^◦

Параметры в форме [A], в свою очередь, могут быть выражены через характеристические параметры:

(17)

,

 

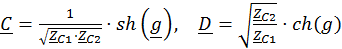где

Для симметричного четырехполюсника:

(18)

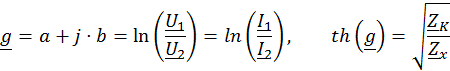
Коэффициент затухания a при этом равен:

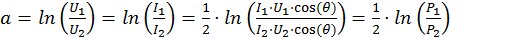(19)

т.к. в данном случае:

Уравнения симметричного четырехполюсника в гиперболических функциях:

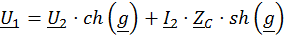
(20)

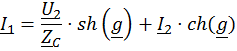
И при согласованной нагрузке: