 |
|
Разложение периодической несинусоидальной кривой в тригонометрический ряд Фурье
Из курса математики известно, что любую несинусоидальную периодическую функцию f(  t) ,удовлетворяющую условиям Дирихле, т.е. имеющую за полный период конечное число максимумов, минимумов и разрывов первого рода, можно представить в виде ряда Фурье
t) ,удовлетворяющую условиям Дирихле, т.е. имеющую за полный период конечное число максимумов, минимумов и разрывов первого рода, можно представить в виде ряда Фурье
f(ωt) = A0 + A1sin(  t+𝜓 1) + A2sin(2𝜔t+𝜓 2) +…. + Aksin(k𝜔t+𝜓 k)+….
= A0 + ∑Aksin(kω+ψk). (2.1)
После раскрытия синуса суммы для каждой из гармонических составляющих ряд Фурье приобретает вид:
A0 + B1sin𝜔t + B2sin2𝜔t +…. + Bksink𝜔t+….
+ C1cos𝜔t + C2cos2𝜔t +…. + Ckcosk𝜔t +….=
A0 + t+𝜓 1) + A2sin(2𝜔t+𝜓 2) +…. + Aksin(k𝜔t+𝜓 k)+….
= A0 + ∑Aksin(kω+ψk). (2.1)
После раскрытия синуса суммы для каждой из гармонических составляющих ряд Фурье приобретает вид:
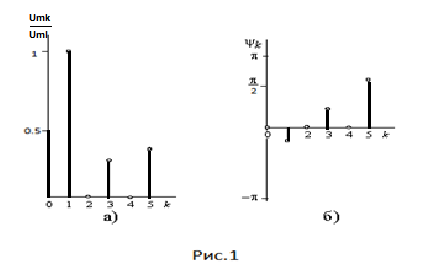
A0 + B1sin𝜔t + B2sin2𝜔t +…. + Bksink𝜔t+….
+ C1cos𝜔t + C2cos2𝜔t +…. + Ckcosk𝜔t +….=
A0 + 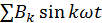 + +  sink sink  t (2.2) t (2.2)
|
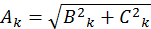 ,
,  ,
,
где
 (2.3)
(2.3)
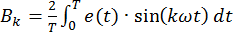 (2.4)
(2.4)
 (2.5)
(2.5)
Первый член ряда A0 называется постоянной составляющей или нулевой гармоникой. Второй член A1sin(  t +𝜓 1) имеет частоту, равную частоте функции f(𝜔t) и называется первой или основной гармонической составляющей (коротко - гармоникой). Остальные члены ряда вида Aksin(k𝜔t+𝜓 k) имеют частоты в целое число раз k больше частоты основной гармоники и называются высшими гармоническим составляющими или гармониками. Каждая высшая гармоника в отдельности именуется по номеру k , т.е. вторая гармоника, третья гармоника и т.д.
t +𝜓 1) имеет частоту, равную частоте функции f(𝜔t) и называется первой или основной гармонической составляющей (коротко - гармоникой). Остальные члены ряда вида Aksin(k𝜔t+𝜓 k) имеют частоты в целое число раз k больше частоты основной гармоники и называются высшими гармоническим составляющими или гармониками. Каждая высшая гармоника в отдельности именуется по номеру k , т.е. вторая гармоника, третья гармоника и т.д.
 Из выражения (2.2) следует, что каждую гармонику ряда Фурье можно представить в виде двух составляющих - синусной Bksink𝜔t и косинусной Ckcosk𝜔t. Амплитуды этих составляющих Bk и Ck называются коэффициентами ряда Фурье.
Из выражения (2.2) следует, что каждую гармонику ряда Фурье можно представить в виде двух составляющих - синусной Bksink𝜔t и косинусной Ckcosk𝜔t. Амплитуды этих составляющих Bk и Ck называются коэффициентами ряда Фурье.
Разложение в ряд Фурье всегда однозначно в отношении постоянной составляющей, а также амплитуд и частот гармонических составляющих. В то же время, начальные фазы гармоник изменяются при изменении момента времени, принятого за начало отсчета. Таким образом, ряд Фурье можно определить, задав номера, амплитуды и начальные фазы гармоник или номера и амплитуды синусной и косинусной составляющих гармоник. Совокупность гармонических составляющих несинусоидальной функции называется дискретным частотным спектром. Спектр можно характеризовать амплитудо-частотной характеристикой(АЧХ) –совокупность амплитуд Ak и фазо-частотной характеристикой (ФЧХ) – совокупность начальных фаз  .Спектры функций удобно изображать отрезками прямых линий, пропорциональных соответствующим величинам. Принято АЧХ строить в относительных единицах:
.Спектры функций удобно изображать отрезками прямых линий, пропорциональных соответствующим величинам. Принято АЧХ строить в относительных единицах:  , выполняя нормировку по амплитуде 1-ой гармоники.
, выполняя нормировку по амплитуде 1-ой гармоники.
Пусть задано напряжение:
u (t)=10+20sin(500t+𝜋 /6)+5sin(1500t+𝜋/4)+7sin(2500t+2𝜋 /3).
Тогда
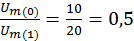
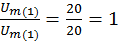

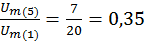
На рисунке 2.1 представлены АЧХ и ФЧХ напряжения u(t).
| Рис. 2.1 |

Для основных типов периодических функций, имеющих геометрически правильную форму - прямоугольную, треугольную, трапециевидную и т.п., выражения для коэффициентов ряда Фурье приводятся в справочниках. Кривые геометрически неправильной формы раскладываются в ряд Фурье графоаналитическим методом с помощью ЭВМ. При проверке полученных результатов разложения в ряд, а также для предварительного исключения из расчетов и анализа коэффициентов, отсутствующих в разложении, полезно отметить некоторые связи между характером периодической функции, и ее частотным спектром. Значительное число непериодических функций времени, с которыми приходится встречаться в электротехнике (рис. 2.2), удовлетворяет условию:
| Рис 2.2 |
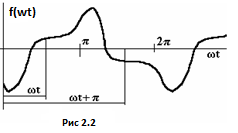
f(𝜔t) = -f(𝜔t+𝜋). (2.6)
Функции, удовлетворяющие этому условию, называются симметричными относительно оси абсцисс. Они раскладываются в ряд, который не содержит четных гармоник и постоянной составляющей:
 +…. =
+…. = 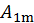 sin(𝜔t+
sin(𝜔t+  +
+
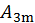 sin(3𝜔t+
sin(3𝜔t+ 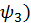 +…. (2.7)
+…. (2.7)
В схемах выпрямления переменного тока часто приходится встречаться с функциями, которые при соответствующем выборе начала координат удовлетворяют условию.
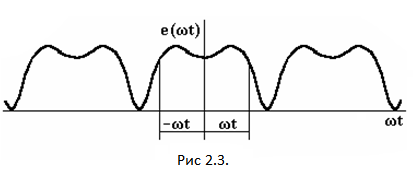
f(𝜔t) =f(-𝜔t). (2.8)
Такие функции называются симметричными относительно оси ординат (рис. 2.3).
В этом случае ряд не содержит синусов:
e (t)=  +
+ 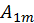 cos𝜔t +
cos𝜔t +  cos2𝜔t +
cos2𝜔t +  cos3𝜔t +…. (2.9)
cos3𝜔t +…. (2.9)
| Рис 2.3 |
схемах умножения частоты встречаются функции, которые при выборе начала координат в точке нуля функции удовлетворяют условию (рис. 2.4).
| Рис 2.4 |

Рис. 2.4
Такие функции называются симметричными относительно начала координат. Они раскладываются в ряд, не содержащий косинусов и постоянной составляющей:
f(𝜔t) = 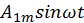 +
+ 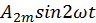 +
+  . (2.11)
. (2.11)
В кривых бывают и несколько видов симметрии одновременно. Для облегчения вопроса о гармонических составляющих в этом случае заполним таблицу 1.
Таблица 1