Главная | Обратная связь

Движение частицы в центральном поле сил.

 

Рассмотрим движение частицы в центральном поле вида U(r) = ,

Где a – константа, которая может быть положительной, либо отрицательной. Положительная константа отвечает случаю отталкивания частицы от силового центра(например, кулоновской силе отталкивания), отрицательная константа – случаю притяжения частицы к центру(кулоновской силе притяжения или силе гравитационного взаимодействия частицы с неподвижной частицей, помещающейся в центре поля)

М=[rp]=const

Векторное произведение перпендикулярно к плоскости, в которой лежат перемножаемые векторы. Отсюда следует, что при неизменном направлении вектора М вектор r всегда лежит в одной плоскости, перпендикулярной к М, и траектория частицы является плоской кривой. Будем определять положение частицы с помощью полярных координат r и φ, совместив начало координат с центром поля. В этих координатах функция Лагранжа имеет вид

L= .

В функцию L не вошла явно координата . Обобщённые координаты, не входящие явно в функцию Лагранжа называются циклическими. В отсутствие непотенциальных сил уравнение Лагранжа, соответствующее циклическим координатам, выглядит следующим образом

(11.2)

Отсюда

. (11.3).

Таким образом, обобщённые импульсы, соответствующие циклическим координатам, оказываются постоянными и являются интегралами движения.

В рассматриваемой нами задаче уравнение 11.2 имеет вид

(11.4)

Для нахождения траектории частицы лучше всего исходить из уравнений 11.3 и 11.4, чем из уравнений Лагранжа. Такой путь проще, так как уравнения Лагранжа содержат вторые производные координат, уравнения же 11.3 и 11.4 – первые производные координат по времени.

Исключив из уравнений 11.3 и 11.4 получим

E= m +

Откуда

=

Из уравнения 11.3

Исключив dt из последних двух уравнений, найдём, что

Введя обозначения 2mE+ = , , -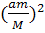

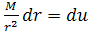
Можно написать

+ , где - постоянная интегрирования.

Возвращаясь к прежним обозначениям, мы получим уравнение траектории частицы в полярных координатах.

(11.5)

Уравнения 11.5 следует, что при заданной величине r разность может иметь 2 отличающихся знаком значения (cos(- )=cos 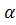). Отсюда легко заключить, что кривая, описываемая уравнением 11.5, симметрична относительно прямой, образующей с осью, от которой отсчитывается угол , угол .

Чтобы выяснить характер кривой, описываемой уравнением 11.5, введём обозначения , (11.6)

=e (11.7)

Тогда уравнение траектории примет вид

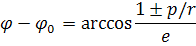
Или после несложных преобразований,

r=± (11.8)

знак соответствует случаю отталкивания, нижний – случаю притяжения частицы к центру сил.

Полученное нами уравнение есть уравнение конического сечения (см. Приложение IV) с фокальным параметром р и эксцентриситетом е.

Рассмотрим сначала случай отталкивания. В этом случае U>0, так что полная энергия Е не может быть отрицательной. Поэтому согласно 11.7 е>1. Таким образом, в случае отталкивания траекторией частицы может быть только гипербола. Получим уравнение траектории

r=

Значение определяется выбором начала отсчёта . Если угол отсчитывать от оси симметрии кривой, то r не должно изменяться при изменении знака . Это имеет место лишь при или . Положив получим уравнение

r=

совпадающее с уравнением IV.14, которое описывает правую ветвь гиперболы(при условии, что начало координат т. е. силовой центр, помещено во внешнем(левом) фокусе гиперболы).

Положив и учтя, что cos( -π)=cos уравнение

 

r= , совпадающее с уравнением IV.13, описывающим левую ветвь гиперболы (при условии, что начало координат помещено во внешнем (правом) фокусе гиперболы рис 11.1).

Теперь обратимся к случаю притяжения (a<0). Ему соответствует в формуле 11.8 нижний знак (плюс). Следовательно уравнение траектории имеет вид

Для =0

r= (11.9)

Для =π

r= (11.10)

Как показано в приложении IV, оба уравнения описывают либо эллипс, либо одну из ветвей гиперболы, либо параболу. С какой из этих кривых мы имеем дело определяется значением е.

В случае притяжения U<0, следовательно полная энергия е может быть как положительной, так и отрицательной, в частности она может оказаться равной нулю. Как следует из формулы 11.7 при Е>0 эксцентриситет оказывается больше единицы и траектория будет гиперболой. Уравнение 11.9 даёт правую ветвь гиперболы, уравнение 11.10 – левую. При этом в отличие от случая отталкивания, начало координат помещается во внутреннем для данной ветви фокусе (рис 11.2).

При Е=0 эксцентриситет оказывается равным единице, и траектория будет параболой. Этот случай осуществляется, если частица начинает своё движение из состояния покоя на бесконечности.

Наконец при Е<0 эксцентриситет меньше единицы, и траектория будет эллипсом. В этом случае кривые, описываемые уравнениями 11.9 и 11.10, отличаются положением силового центра. Кривая 11.9 получается, если центр сил помещается левом фокусе эллипса. Кривая 11.10 соответствует расположению центра сил в правом фокусе.

Лекция 6