 |
|
Четырехмерные векторы и тензоры в псевдоевклидовом пространстве
2. Многомерный вектор
Квадрат радиус-вектора определяется как
x12 + x22 + … + xn2 = S xi2 (1)
Если ввести тензор вида
 gij = dik =
gij = dik = 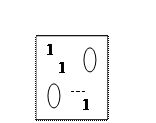 - метрический тензор. (2)
- метрический тензор. (2)
то(1) записываем в виде
для i , k =1,n
S gik xi xk (3)
В специальной теории относительности и электродинамике уравнения приобретают простой вид, если их представить в виде соотношений между векторами и тензорами в четырехмерном пространстве, метрика которого определяется тензором
Лекция №8
 - метрика «псевдоевклидового» пространства (4)
- метрика «псевдоевклидового» пространства (4)
Пространство, свойства которого определяются тензором(4) называется псевдоэвклидовым
Индексы пробегают значения μ, ν = 0,1,2,3
Индексы латинские ijk – латинские для векторов в обычном з-х мерном пространстве(в пространстве с эвклидовой метрикой)
(xo,x1,x2,x3) – 4-прстранство
Обозначения
xo = ct ; x1 = x; x2 = y; x3 = z
действие матричного оператора на вектор- в результате вектор
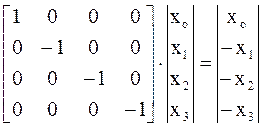 - вектор четырехмерного пространства
- вектор четырехмерного пространства
Выражение для результирующего вектора имеет вид
r = ct – x – y – z
алгебраическая запись действия матричного оператора
x=  / = ct/ - x1/ - x2/ - x3/
/ = ct/ - x1/ - x2/ - x3/
Любой вектор можно преобразовать, записывая матрицу преобразования.
Определение квадрата радиуса-вектора в 4- пространстве
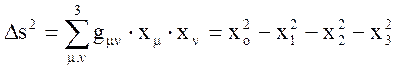 - инвариант
- инвариант
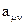 - матрица прямого преобразования(обратное-матрица с чертой)
- матрица прямого преобразования(обратное-матрица с чертой)
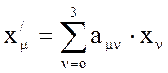 - прямое преобразование (8)
- прямое преобразование (8)
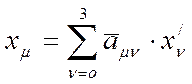 - обратное преобразование
- обратное преобразование
Используя свойство инвариантности квадрата 4-радиус-вектора(интервала) запишем
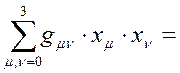
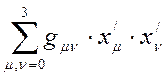
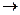
подставим 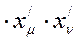 из(8)
из(8)
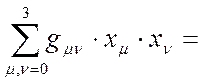
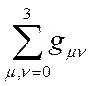
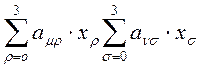 (11)
(11)
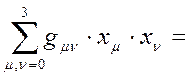
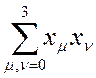
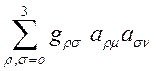 (12)
(12)
после преобразований получим условие для линейного преобразования
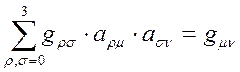 (13)
(13)
Учитывая, что в отличны от нуля только диагональные члены
(13) препишем в упрощенной форме
 m,n= 0,1,2,3 (14)
m,n= 0,1,2,3 (14)
например при m,n= 0, 1- при m,n= 0, 2-при m=1, n=2
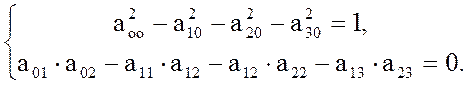 (15)
(15)
(16)
1,2 – следствия из условия неинвариантности
Связь между прямым и обратным преобразованием:
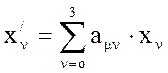 ; -прямое преобразование (17)
; -прямое преобразование (17)
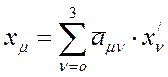 -обратное преобразование
-обратное преобразование
где 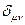 =1 коэффициент - символ Кронекера - единичная матрица
=1 коэффициент - символ Кронекера - единичная матрица
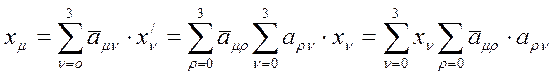 (18)
(18)
Компоненту можно представить в виде

Тогда можно записать
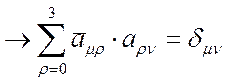 m,n= 0,1,2,3 (20)
m,n= 0,1,2,3 (20)
Система справедлива(удовлетворяется) если положить
1) 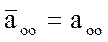
2)  (21)
(21)
3) 
4) 
i,k = 1,2,3,
например, при m=n= 0 уравнение(20) выглядит в виде
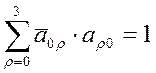 (22)
(22)
С учетом (21)
a00a00 -∑13 ai0ai0 =1 (23)
что аналогично (15)
При m=1, n= 2
∑13 a1ρaρ2 =0 (24)
Откуда с учетом (21)
-a10a02 +∑13 ai1ai2 =0 - что похоже на (16)
Условие (21) можно записать в виде

При m=0, n= 0
a'00 = a00 (g00 =g00=1)
При m=0, n= i ≠0 как и при m=i≠0, n= 0
будет выполняться
gμμ =-gνν , т.е. -1
Поэтому
a'0i = -ai0
и
a'i0 = -a0i
А при m = i ≠ 0, n= k ≠ 0
Оба множителя равны -1
gμμ =gνν = -1
так, что
a'ik = aki
(что в (21))
В теории относительности рассматриваются преобразования, когда координаты x2=y, x3 =z остаются неизменными(выбор координат специально по движению вдоль оси x, когда переменными остаются время t и x)
Очевидно, что матрица преобразования, имеет вид
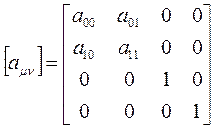
Обратное преобразование имеет вид, аналогичный
В системах отсчета K и K' матрицы отличаются на некий параметр р(например, поворот или относительная скорость V). В пределе при p->0 матрицы совпадут
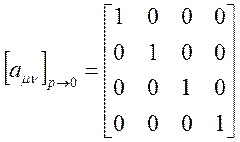
limp->0 a00 =lim p->0a11 =1
limp->0 a01 =lim p->0a10 =0
Записав(14) для m=0, n= 0
a200 - a210 =1 (28)
Для обратного преобразования
a'200 - a'210 =1
С учетом взаимосвязи прямого и обратного преобразования(21)
a200 - a201 =1 (30)
Из (28) и (30) следует
a210 = a201
и извлекая корень
a10 = _+ a01
Теперь(14) при m=0, n= 1 получим
a00 a01 - a10 a11 =0,
откуда при
a10 = a01
1. a00 = a11
2. a00 = -a11, если a01 = a10
a00 = a11
a10 = - a01
Учитывая, что справедливы соотношения
limp->0 a00 =lim p->0a11 =1
то справедлив первый вариант. Тогда следует считать
a00 = a11=γ0
a01 = a10=γ1
Тогда (26) перепишем в виде
Отсюда следует:
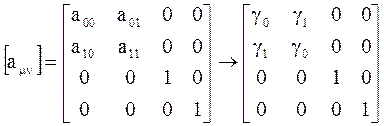 ,
,
причем
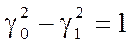
Поскольку
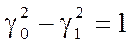 ,
,
только один коэффициент является независимым.
Коэффициенты обратного преобразования связаны соотношениями(21)
a'00 = a00=γ0
a'01 = -a10=γ1
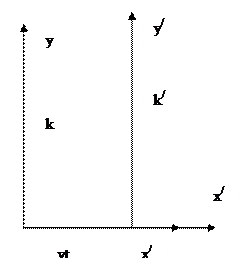
То есть координата x меняются; y,z – const
Тогда матрица обратного преобразования может быть представлена в виде
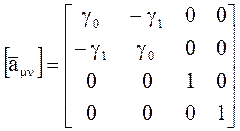
Таким образом, рассмотрены основные свойства преобразований 4-вектров, которые используются при формировании математического аппарата преобразований основных показателей(уравнений движения) для движущихся систем-преобразования Лоренца