Главная | Обратная связь

Преобразования Лоренца

Интервал инвариантен при геометрических преобразованиях в 4-пространстве, т.е. подобен модулю вектора в евклидовом пространстве

 

x_o = ct ; x₁ = x; x₂ = y; x₃ = z

 

Квадрат интервала

 

ds² = c²d t² – dx² – dy² – dz² = c²d t² - dl²

 

dl² = dx² + dy² + dz² – inv (инвариантв евклидовом пространстве) – модуль разности векторов точек.

x_o ; x₁; x₂; x₃ –координаты –компоненты 4-радиуса-вектора мировой точки.

пространство, где события изображаются мировой точкой с такими координатами, обладает псевдоевклидовой метрикой, определяемой тензором

 

Пространство, свойства которого определяются тензором(4) называется псевдоэвклидовым

 

- метрика «псевдоевклидового» пространства (4)

 

Преобразование компонент 4-радиус-вектора осуществляется по формуле

где матрица преобразования

,

причем

 

Поскольку , только один коэффициент является независимым.

Рассмотрим системы отсчета обеих К и К' систем отсчета, движущихся относительно друг друга со скоростью v.

Преобразование нулевого вектора

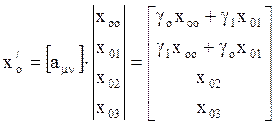
Для преобразованных величин получаем

 

или

для нулевой координаты x' =0, x=vt:

из получаем, что

; ; ;

 

- коэффициент преобразования Лоренца

;

;

Подстановка в формулу преобразования координат 4-вектора дает

; ; где

Формулы обратного преобразования получаются аналогично с учетом, того что перед коэффициентом стоит знак плюс.

 

Переходя к обычным обозначениям для прямого преобразования

;

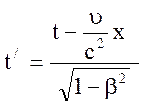
; y^/ = y; z^/ = z;

Обратные преобразования реальных координат

; ;

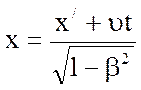Преобразования Лоренца оставляют интервал инвариантным(проверить!!!) Сокращение размеров и вариация объема

;

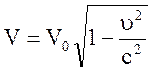
Все эти преобразования осуществляются при изменении одной координаты х.

Преобразование скорости

дифференцируя формулу прямогопреобразования

;

- преобразование скоростей

;

Обратные преобразования получаются аналогично