 |
|
Геометрический смысл преобразования Лоренца

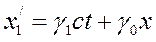
Это линейное преобразование напоминает преобразование поворота в трехмерном евклидовом пространстве. Это преобразование, характеризующее поворот плоскости xy на угол φ в обычном пространстве выглядит в виде

При таком, сравнении получим, что

Очевидно не существует действительного угла  , который удовлетворял бы этим соотношениям. Однако, как легко видеть, существует чисто мнимый угол
, который удовлетворял бы этим соотношениям. Однако, как легко видеть, существует чисто мнимый угол 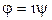 , для которого приведенные соотношения будут выполняться. Действительно,
, для которого приведенные соотношения будут выполняться. Действительно,

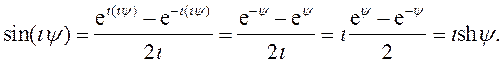
Поэтому, как следствие вышеприведенных соотношений, получаем формулы
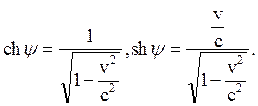
Данные соотношения разрешимы, так как, согласно им,

Как видим, значение мнимого угла 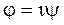 , определяется значением отношения скоростей
, определяется значением отношения скоростей  . Введем теперь действительную временную координату
. Введем теперь действительную временную координату  , для которой
, для которой  , или
, или 
Тогда формулы преобразования Лоренца примут вид

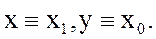
Это формулы так называемого гиперболического поворота
Преобразование динамики (уравнения Ньютона) для четырехмерного пространства:
 ; i = 1,2,3 – для евклидового пространства
; i = 1,2,3 – для евклидового пространства
В случае релятивистской механики уравнения движения записываются для вектора скорости, полученного после преобразований с учетом инвариантности
Четырехмерное обобщение имеет вид
 где m = 0,1,2,3 – релятивистская динамика
где m = 0,1,2,3 – релятивистская динамика
Здесь время является собственным временем наблюдателя. Масса-инвариантная величина, характеризующая инертные свойства частицы. Аналог силы-сила Минковского должна быть определена т.о., чтобы при малых скоростях она переходила в обычное уравнение движения.
В нерелятивистской механике dl, dt являются inv поэтому v=dr/dt – скорость, а ускорение a=dv/dt
Релятивистские dl и dt ≠ inv
inv является интервал ds, связанный с dl и dt. При этом
ds2 = c2 dt2-dl2
Основная задача найти 4-х мерные аналоги 3-вектора –четырехмерную скорость частицы v и ускорение a.
Родственное dt - собственное время dτ =ds/c→ inv
 ; -свойства 4-вектора для четырехмерной скорости частицы
; -свойства 4-вектора для четырехмерной скорости частицы
Для ускорения имеем формулу
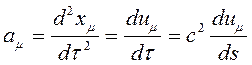
Нулевая компонента скорости
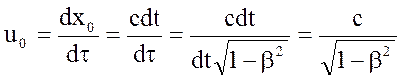 ;
;
Остальные компоненты скорости

Векторная запись имеет вид

При скоростях много меньших скорости света получаем обычную скорость.
закон Ньютона для нулевой компоненты запишем

Для остальных компонент
 , где i = 1,2,3 – сила Минковского
, где i = 1,2,3 – сила Минковского
Сила Минковского связана с Ньютоновской силой соотношением

Иначе закон движения можно записать

Для квадрата 4-вектора справедливо соотношение
 где
где
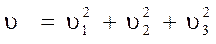
Для определения временной компоненты силы Минковского умножим уравнение движения на скорость.
Домножая уравнение движения на вектор скорости

Просуммируем
 , то есть вектор скорости перпендикулярен направлению. Здесь учтено
, то есть вектор скорости перпендикулярен направлению. Здесь учтено
 ,
,
Подставляем выражение для скорости и силы Минковского и, расписывая сумму, получим

Откуда

Тогда вектор силы Минковского будет представлен компонентами

Скалярное произведение силы на скорость- есть работа совершенная частицей в единицу времени, равная изменению энергии частицы


Интегрируя данное уравнение, получим
 , где const = 0;
, где const = 0;
Константу определил Эйнштейн и экспериментально подтвердил
Для снеподвижного тела справедливо выражение для энергии
E=mc2 – уравнение Эйнштейна.
Это уравнение выражает энергию покоя частицы.
∆m = ∆E/c2
Покоящийся электрон и позитрон испускают два γ-кванта с суммарной энергией равной сумме энергий покоя электрона и позитрона.