 |
|
Интегрирование иррациональных и трансцендентных функций.
Предварительно введем понятие рациональной функции от двух переменных u и v, то есть функции получающейся из этих переменных и некоторых постоянных, над которыми производятся только операции сложения, вычитания, умножения и деления R(u, v). Такова, например, функция
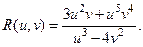
Если переменные u и v, в свою очередь являются функциями переменной x:  то функция
то функция 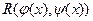 называется рациональной функцией от
называется рациональной функцией от 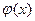 и
и 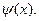
Рассмотрим теперь интегралы от некоторых простейших иррациональных и трансцендентных функций сводящихся к интегралам от рациональных функций.
1. Интегралы вида 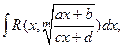 где a, b, c, d – некоторые числа
где a, b, c, d – некоторые числа 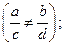 m – натуральное число. Интегралы данного вида рационализируются подстановкой
m – натуральное число. Интегралы данного вида рационализируются подстановкой 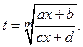
2. Интеграл вида 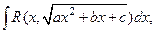 где a, b, c – некоторые числа
где a, b, c – некоторые числа 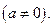 Данный интеграл зависит от корней квадратного трехчлена
Данный интеграл зависит от корней квадратного трехчлена 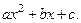 Если этот трехчлен имеет два различных действительных корня x1 и x2, то он сводится к интегралу вида 1, а именно к интегралу
Если этот трехчлен имеет два различных действительных корня x1 и x2, то он сводится к интегралу вида 1, а именно к интегралу
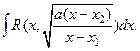
Если x1=x2, то интеграл сводится к интегралу от рациональной функции, а именно к интегралу
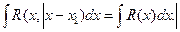
Если же квадратный трехчлен не имеет вещественных корней, то с помощью подстановки Эйлера

данный интеграл приводится к интегралу от рациональной функции

3. Интеграл вида  рационализируется подстановкой
рационализируется подстановкой  Действительно,
Действительно,
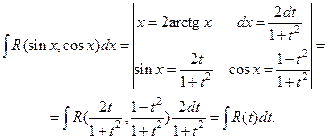
4. Интеграл вида 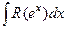 рационализируется подстановкой
рационализируется подстановкой 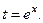 Действительно,
Действительно,
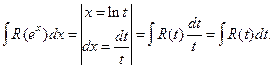
Практическое занятие 17
Непосредственное интегрирование
Нахождение неопределенных интегралов с помощью таблицы, основных свойств неопределенных интегралов и тождественных преобразований подынтегральных функций называется непосредственным интегрированием.
Пример.Найти неопределенный интеграл 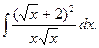
Решение.Выражение в числителе возведем в квадрат и разделим полученное выражение на знаменатель. Применяя таблицу интегралов и их свойства, будем иметь:
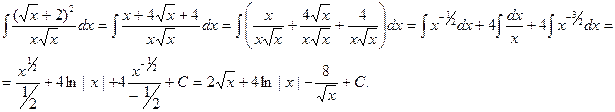
Упражнения
1. 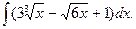 2.
2. 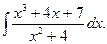
3. 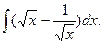 4.
4. 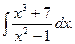
5.  6.
6. 
7. 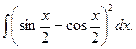 8.
8. 
9.  10.
10. 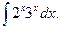
11. 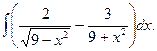 12.
12. 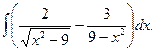
13. 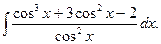 14.
14. 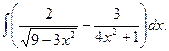
15. 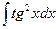 16.
16. 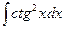
17. 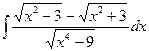
 18.
18. 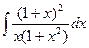
19. 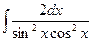 20.
20. 