 |
|
Смешанные задачи на интегрирование
1.  2.
2. 
3  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 
15.  16.
16. 
Контрольная работа по теме «Неопределенный интеграл»
Вариант 1
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10. 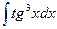 .
.
11.  . 12.
. 12.  .
.
Вариант 2
1.  . 2.
. 2. 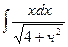 .
.
3. 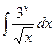 . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
11.  . 12.
. 12.  .
.
Вариант 3
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9. 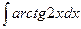 . 10.
. 10.  .
.
11.  . 12.
. 12.  .
.
Вариант 4
1.  . 2.
. 2.  .
.
3.  . 4.
. 4. 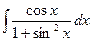 .
.
5.  . 6.
. 6. 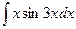 .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
11.  . 12.
. 12.  .
.
Вариант 5
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
6.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
11.  . 12.
. 12.  .
.
Вариант 6
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
11.  . 12.
. 12.  .
.
Вариант 7
1.  . 2.
. 2.  .
.
3.  4.
4.  .
.
5.  . 6.
. 6.  .
.
6.  . 8.
. 8.  .
.
9. 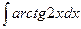 . 10.
. 10.  .
.
11.  . 12.
. 12.  .
.
Вариант 8
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
6.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
11.  . 12.
. 12.  .
.
Вариант 9
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
6.  . 8.
. 8.  .
.
9.  . 10.
. 10.  .
.
11.  . 12.
. 12.  .
.
Вариант 10
1.  . 2.
. 2.  .
.
3. 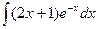 . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
6.  . 8.
. 8. 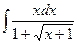 .
.
9.  . 10.
. 10.  .
.
11.  . 12.
. 12. 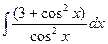 .
.
НЕДЕЛЯ 10
Лекция 19
Определенный интеграл. Условия существования
Определенного интеграла. Свойства определенного интеграла.
Задача о поиске площади криволинейной трапеции приводит к понятию определенного интеграла. Криволинейная трапеция ограничена осью Ох, непрерывной функцией y=f(x), прямыми x=a и x=b, т.е. трапеция расположена над осью Ох. Разделим основание трапеции ¾ интервал [a,b] на n частичных интервалов [x0,x1],[x1,x2],…,[xn-1,xn], где a=x0<x1<x2<…<xn-1<xn=b.
Проведя в точках деления [a,b] прямые, параллельные оси ординат, разобьем криволинейную трапецию на n частичных трапеций. В каждом частичном интервале возьмем точки x1,x2,…,xт, так что
x0£x1£x1, x1£x2£x2, …, xn-1£xn£xn.
Рассмотрим значения ¦(x1),¦(x2),…,¦(xn) и т.д.
В результате, сложив площади всех частичных трапеций, получим площадь криволинейной трапеции
S=  Sn=
Sn= 
 ¦(xi)Dxi, где Dxi=xi-xi-1.
¦(xi)Dxi, где Dxi=xi-xi-1.
 ¦(xi)Dxi называется n-й интегральной суммой.
¦(xi)Dxi называется n-й интегральной суммой.

 ¦(xi)Dxi=
¦(xi)Dxi=  ¦(x)dx называется определенным интегралом, a-нижний предел интегрирования, b- верхний предел интегрирования.
¦(x)dx называется определенным интегралом, a-нижний предел интегрирования, b- верхний предел интегрирования.
Определенным интегралом называется предел, к которому стремится интегральная сумма при стремлении к нулю длины наибольшего частичного интервала.
Теоремасуществования определенного интеграла. Если функция ¦(x) непрерывна в замкнутом интервале [a,b], то ее n-я интегральная сумма стремится к пределу при стремлении к нулю длины наибольшего частичного интервала. Этот предел, т.е. определенный интеграл  ¦(x)dx, не зависит от способа разбиения интервала интегрирования на частичные интервалы и от выбора в них промежуточных точек.
¦(x)dx, не зависит от способа разбиения интервала интегрирования на частичные интервалы и от выбора в них промежуточных точек.