 |
|
Дифференциальные уравнения I порядка.
Понятие о дифференциальном уравнении.
Теория дифференциальных уравнений широко используется в естествознании и технике. В частности, при решении многих физических задач приходится находить неизвестную функцию по данному соотношению между неизвестной функцией, ее производными и независимыми переменными.
С формальной точки зрения задача решения дифференциального уравнения есть задача, обратная дифференцированию. Однако в теории дифференциальных уравнений приходится не только интегрировать заданное дифференциальное уравнение для отыскания искомой функции, но и зачастую по условию той или иной задачи составлять это уравнение и затем решать его.
Дифференциальным называют такое уравнение, в котором неизвестной является функция одной или нескольких переменных, причем в уравнение входит не только сама функция, но и ее производные.
Если неизвестная функция является функцией одной независимой переменной, то уравнение называется обыкновенным дифференциальным, если же – функцией нескольких переменных, то – дифференциальным уравнением в частных производных.
Порядок наивысшей производной (или дифференциала), входящей в дифференциальное уравнение, называется порядком уравнения.
В общем виде обыкновенное дифференциальное уравнение 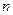 -го порядка можно записать так:
-го порядка можно записать так:
 .
.
Например,  есть дифференциальное уравнение второго порядка.
есть дифференциальное уравнение второго порядка.
Любая функция, удовлетворяющая дифференциальному уравнению, называется решением или интегралом этого уравнения.
Решение дифференциального уравнения (если оно существует), в котором число произвольных постоянных равно порядку уравнения, называется общим решением данного дифференциального уравнения.
Общее решение обыкновенного дифференциального уравнения 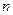 -го порядка записывается так:
-го порядка записывается так:
 .
.
Решения дифференциального уравнения при определенных значениях произвольных постоянных называется частным решением. Условия, которым должно удовлетворять искомое частное решение данного дифференциального уравнения, называются начальными условиями. Задача отыскания конкретного частного решения данного дифференциального уравнения по начальным данным называется задачей Коши.
Так как каждое частное решение данного дифференциального уравнения есть некоторая функция одной переменной, то в прямоугольной системе координат на плоскости этому решению соответствует некоторая линия. Она называется интегральной кривой данного дифференциального уравнения. Общему же решению дифференциального уравнения соответствует множество всех интегральных кривых этого уравнения, которое называется семейством интегральных кривых дифференциального уравнения.
Дифференциальным уравнением первого порядка называется уравнение вида: 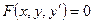 или
или 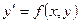 . Его общее решение содержит одну произвольную постоянную С:
. Его общее решение содержит одну произвольную постоянную С:  .
.
Дифференциальные уравнения первого порядка иногда удобно записывать и в виде:
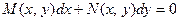 .
.
Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения.
Если функции 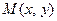 и
и  разлагаются на множители:
разлагаются на множители:  , а
, а  , тогда уравнение вида:
, тогда уравнение вида:

называется уравнением с разделяющимися переменными.
Предположив, что 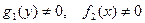 , и разделив обе части первого уравнения на
, и разделив обе части первого уравнения на  , получим уравнение с разделенными переменными:
, получим уравнение с разделенными переменными:
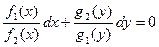 ,
,
которое интегрируется:
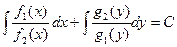 .
.
Вычисление полученных интегралов и дает общее решение уравнения с разделяющимися переменными.
Функция 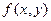 называется однородной функциейизмерения
называется однородной функциейизмерения  (
(  ) относительно аргументов х и у, если равенство
) относительно аргументов х и у, если равенство  справедливо для любого
справедливо для любого  , при котором функция
, при котором функция  определена.
определена.
Если  , то функция будет однородной нулевого измерения
, то функция будет однородной нулевого измерения 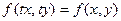 .
.
Дифференциальное уравнение первого порядка 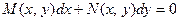 называется однородным,если
называется однородным,если 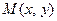 и
и  - однородные функцииот х и у одинакового измерения, т.е.
- однородные функцииот х и у одинакового измерения, т.е. 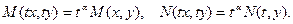 Действительно, переписав его в виде:
Действительно, переписав его в виде:  легко заключаем, что
легко заключаем, что 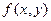 - однородная функция нулевого измерения, поскольку:
- однородная функция нулевого измерения, поскольку:
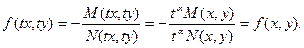
Так как однородное дифференциальное уравнение первого порядка всегда можно записать в виде  то, положив
то, положив  , получим:
, получим:

Данное уравнение решается с помощью замены  и сводится к уравнению с разделяющимися переменными относительно х и новой функции
и сводится к уравнению с разделяющимися переменными относительно х и новой функции  :
:
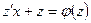 . Отсюда следует:
. Отсюда следует: 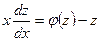 . Разделив переменные и выполнив почленное интегрирование, находят общее решение однородного дифференциального уравнения первого порядка.
. Разделив переменные и выполнив почленное интегрирование, находят общее решение однородного дифференциального уравнения первого порядка.
Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли.
Дифференциальное уравнение первого порядка:
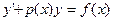
называется линейным, если оно линейно относительно неизвестной функции у и ее производной  , где
, где 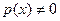 и
и  - непрерывные функции от х.
- непрерывные функции от х.
Линейное дифференциальное уравнение первого порядка называется однородным, если  , в противном случае оно неоднородное.
, в противном случае оно неоднородное.
Линейное дифференциальное уравнение можно проинтегрировать методом Бернулли, суть которого заключается в следующем. Представим искомую функцию  в виде произведения двух неизвестных функций
в виде произведения двух неизвестных функций  и
и  по формуле
по формуле 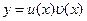 (подстановка Бернулли).Тогда
(подстановка Бернулли).Тогда  Подставив выражения для у и у’ в линейное дифференциальное уравнение, получим:
Подставив выражения для у и у’ в линейное дифференциальное уравнение, получим:
 ,
,
которое преобразуем к виду:
 .
.
Так как 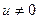 , то интегрирование данного вида уравнения сводится к интегрированию двух уравнений с разделяющимися переменными:
, то интегрирование данного вида уравнения сводится к интегрированию двух уравнений с разделяющимися переменными:
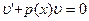 и
и 
Найдя общее решение  изпервого уравнения, а затем и
изпервого уравнения, а затем и 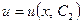 из второго уравнения, придем к общему решению линейного уравнения:
из второго уравнения, придем к общему решению линейного уравнения: 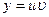 .
.
Дифференциальное уравнение
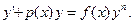
где  , называется уравнением Бернулли.
, называется уравнением Бернулли.
Путем введения новой функции  по формуле
по формуле  , откуда
, откуда  , уравнение Бернулли сводится к линейному уравнению относительно этой функции:
, уравнение Бернулли сводится к линейному уравнению относительно этой функции:

Уравнение Бернулли, как и линейное уравнение можно решить с помощью подстановки Бернулли 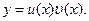
Лекция 22